たしざんの計算方法(整数の普通の計算)
学習する学年:小学生
1.整数のたしざんについて
たしざんは、普段の生活の中で毎日のように使う機会がありますよね。
たしざんとは、数と数を足し合わせて合計を求める計算方法のことです。
例えば、スーパーで買い物をする時に、パン100円、ジュース98円の品物を購入する時は、100円+98円=198円というようにたしざんをして合計金額を計算しています。
また、財布のお金を数える時にもたしざんは使います。小銭入れに500円玉が1枚、10円玉が6枚、1円玉が9枚入っていたら、500円+60円+9円=569円というようにたしざんを使えば合計金額が計算できます。
このように、たしざんは普通に数を加えていけばいいので、小学生の方でも簡単に計算できるのではないでしょうか。
ここでは、1つ目は1ケタの整数どうしのたしざん、2つ目は2ケタの整数と1ケタの整数のたしざん、3つ目は2ケタの整数どうしのたしざんの計算方法を見ていきましょう。
2.1桁の整数どうしのたしざんの計算方法
1ケタの整数どうしのたしざんとは、1ケタの整数と1ケタの整数を足し合わせる計算のことです。
それでは、次の式の1ケタの整数どうしのたしざんの計算をやってみましょう。
- 9+9=
1ケタの数どうしの計算では、そのまんまそれぞれの数を目で見て暗算でぱっと答えが思い浮かぶと思いますし、思い浮かばなかったら指を使って計算すれば簡単ですね。
暗算する時のコツは、次のように9を分解して1+8にしてから計算するとわかりやすくなります。
9+9=を計算するより、9+(1+8)=にした方がわかりやすいと思いませんか?
- 9+9=9+(1+8)=10+8=18
1ケタの数どうしの計算は特に筆算(ひっさんとは、紙に数字を書いて計算すること)に置き換える必要はありませんが、9+9の式を、下のように筆算に置き換えて計算してみます。
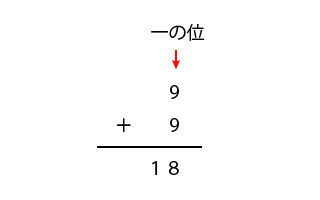
筆算に置き換える時の注意点は、それぞれの数の位を揃えることです。この場合は1ケタの数どうしなので、一の位に合わせて計算します。
筆算でたしざんを計算すると、一の位は8、十の位は一の位からの繰り上がりがあるので1となります。
よって、9+9の答えは18となります。
3.2桁の整数と1桁の整数のたしざんの計算方法
次の式の2ケタの整数と1ケタの整数のたしざんの計算をやってみましょう。
- 38+5=
暗算で計算する時は、次のように5を分解して2+3にしてから計算するとわかりやすくなります。
- 38+5=38+(2+3)=40+3=43
この数の計算は暗算で計算できそうですが、紙に書いて筆算で計算してみましょう。
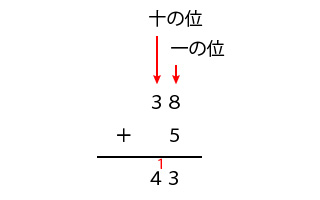
筆算に置き換える時の注意点は、それぞれの数の位を揃えることなので、この場合は1ケタの数は2ケタの一の位に合わせて計算してください。
筆算でたしざんを計算すると、一の位の足し算は、8+5=13なので一の位は3になり、十の位に1が繰り上がります。
十の位には3がありますので、下の位から繰り上がってきた1を足すと3+1=4になります。
よって、38+5の答えは43となります。
たしざんを計算する時のコツは、繰り上げた数は小さい字で各位に数を書いて計算ミスを少なくすることです。
4.2桁の整数どうしのたしざんの計算方法
2ケタの整数どうしのたしざんとは、2ケタの整数と2ケタの整数を足し合わせる計算のことです。
それでは、次の式の2ケタの整数どうしのたしざんの計算をやってみましょう。
- 63+77=
上の式の数をぱっと見て答えはわかりますか?
暗算で計算する時は、次のように77を分解して70+7にしてから計算するとわかりやすくなります。
- 63+77=63+(70+7)=63+7+70=70+70=140
もしわからなかったら、63+77の式を下のように筆算に置き換えて紙に書いて計算してください。
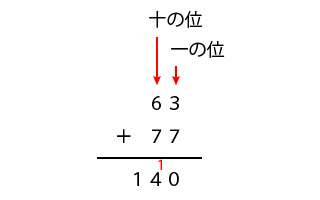
筆算に置き換える時の注意点は、それぞれの数の位を揃えることでしたよね。この場合は2ケタの数どうしなので、十の位と一の位に合わせて計算します。
筆算でたしざんを計算すると、一の位の足し算は、3+7=10なので一の位は0になり、十の位に1が繰り上がります。
※繰り上げた数は小さい字で各位に書いておきましょう。
十の位の足し算は、6+7=13です。この13の数に、下の位から繰り上がってきた1を足すと14になります。
よって、十の位で計算して導いた14と一の位で計算して導いた0を連結して、答えは140になります。
整数の足し算は簡単に計算できたのではないでしょうか。
5.計算を早くするおすすめの本
計算力が身についていない方はいませんか。足し算、引き算、掛け算、割り算の計算が早くなるおすすめの本を紹介します。
本の名前:大人のための「超」計算 正しく 速く カッコよく解く
大人のための「超」計算は、お子さんではなく大人の方の為の計算力が早くなる本です。
日常生活では、足し算、引き算、掛け算、割り算を普通に使いますよね。四則演算を速く計算するにはコツがあります。
論理的なコツがいろいろ書いてありますので、今まで遅かった計算力を速くした方は1度読んでみてください。計算力が身につきますよ。

