原始関数
学習する学年:高校生
1.原始関数の説明
原始関数とは、積分を扱う上で理解していなければいけない初歩的な語句です。
原始関数とは、関数y=f(x)を積分したy=F(x)をさらに微分すると元の関数y=f(x)になるもののこと。微分の逆演算をすることで求めることができる関数のことです。
※導関数した数を積分した関数、微分する前の関数は原始関数に当てはまります。
上の言葉の説明をまとめると下のようになります。
関数F(x)を微分した導関数がf(x)であるとき、F(x)はf(x)の原始関数といいます。
例えば、2xという原始関数を考えてみましょう。
関数F(x)を微分すると2xになれば原始関数となるので、x2、x2+3、x2-5などは原始関数となります。
原始関数は1つだけあるのではなく、たくさんあることに気が付きませんか。
そうなんです、定数が異なる原始関数はたくさんあるのでF(x)+定数としても表わすことができます。
また、わかりやすいように定数部分を記号のCに置き換えてみませんか。原始関数の定数部分にCを付け加えたものであるF(x)+Cという式も原始関数といいます。
したがって、2xという原始関数は、
- x2+C
となり、Cを使うことによって全ての原始関数を表すことができます。
このCという記号は、積分定数(せきぶんていすう)と言われていて定数のゲタ(高さ)みたいな意味を表現しています。
なぜこのCという記号を付けないといけないのかというと、元の関数には何か他の定数(情報)がくっついていたのではないかという推測をしているからです。
つまり、原始関数とは、F(x)+Cとなる数のことを言っています。必ず積分定数Cを忘れずにつけてください。
2.原始関数をグラフに表してみましょう
原始関数をわかりやすく理解する為に、下図のようなy=f(x)のグラフを描いてみます。
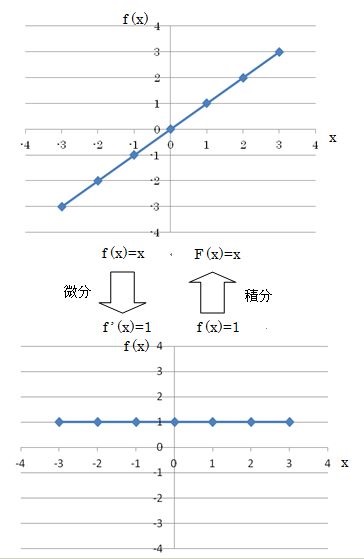
上のグラフを説明すると、
- 関数f(x)=xを微分すると、導関数f'(x)=1
- 導関数f(x)=1を積分すると、原始関数F(x)=x+C
になります。
原始関数は、微分の逆演算をすると求まる関数であるという事は、関数を積分すれば原始関数が導けるという事になります。
したがって、関数f(x)=1を積分して出てきたx+Cは原始関数になります。
積分(不定積分)を行う時は積分定数Cを考慮しなければいけないので、x+0でも、x+1でも、x+2でも、x+10でもゲタ(高さ)の役割をするCを加えて原始関数x+Cにしなければいけないということを覚えてください。
微分や積分に出てくる言葉は、難しくて取っ付きにくいものが多いですが頑張って理解しましょう。
