比｜もう一度やり直しの算数・数学

比

学習する学年：小学生

比とは、簡単に説明すると2つ以上の数や量の大きさの関係を表したものです。

これだけの説明ではわからないですよね。どういうことかというと、例えば、ハンバーガーの値段はチロルチョコの値段よりも5倍高いならば、5：1の関係があります。

ハンバーガーとチロルチョコの値段の比は5：1とは、ハンバーガーが100円ならチロルチョコは20円ということです。

つまり、上記の比はハンバーガーはチロルチョコよりも5倍値段が高いということを表しています。

さぶろう君の体重が25kg、さぶろう君のお母さんの体重が50kgならば、25：50、それぞれを25で割って1：2の関係があります。

さぶろう君とさぶろう君のお母さんの体重の比は1：2とは、さぶろう君よりもお母さんの体重は2倍重たいということです。

比を表す時に使う：の記号は対（たい）といい、5：1（ごたいいち）、1：2（いったいに）のような何対何の関係を比といいます。

比を使う時に注意することは一番小さい数で表すことがルールです。このような比を使うことで、あるものとあるものの数や量の関係が比べやすくできます。

では、算数・数学の授業で比はどういう時に活用すればいいのでしょうか？

みなさんはこのようなことを聞いたことはありませんか。2つの図形があってこの図形とあの図形は相似比（そうじひ）がいくつでとか、この図形はあの図形を拡大したものとか。そのような場合は比の関係を用いて計算するとわかりやすくなります。

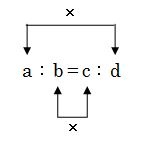
比は、外項と内項で成り立っていて、a：b＝c：dで表されることがあります。

a：b＝c：dの言い方は、a対b＝c対d、aたいbイコールcたいdといいます。

外項と内項を簡単に説明すると次のようになります。

そして、外側の数どうしを掛け合わせた値と内側の数どうしを掛け合わせた値は同じ値になるという関係があります。

つまり、外項の積＝内項の積、外項の積と内項の積は等しいという性質があります。

上の図で説明すると、a、b、c、dという数があり、その数は、a：b=c：dが成り立つ時は、ad＝bcとなります。

このような、a：b＝c：dという比の式を比例式といいます。

外項の積、内項の積数といわれてもよくわからないと思いますので、比をわかりやすく理解するために図形を使って説明します。

下に２つの四角形があります。この2つの四角形の辺の長さの比は等しい関係にあったとすると、Xの値はいくらになるでしょうか？

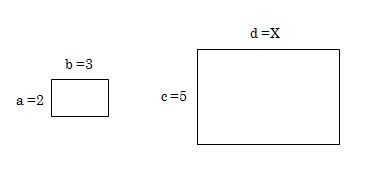
それぞれの四角形の長さの比は等しいので、上記で説明した比例式のa：b=c：dが成り立ちます。

ですので、外項の積と内項の積を使って計算してみましょう。

それでは、a、b、c、dに四角形のそれぞれの辺の値を当てはめまてみると、2：3＝5：Xとなります。

比例式が完成しましたので、外項の積と内項の積の計算を始めます。

比の関係が成り立つとは、外項の積と内項の積の値が等しくなるということなので、2X＝15という関係が導きだされます。

したがって、Xについて計算すると、

となります。

比の関係を使えば図形の辺の長さなどが計算できるようになります。