1次方程式の成り立ち
学習する学年:中学生
1.方程式の説明
小学校を卒業して中学1年生になると方程式の授業が始まります。
中学校の数学の時間に、1次方程式や2次方程式を解きましょうとよく耳にしたと思いますが、みなさんは方程式の授業の内容は覚えていますか?
方程式は2x+y=1というようなxやyというアルファベットが含まれている等式だと覚えていた方は正解です。
もう少し具体的に説明しますと、xやyは未知数という意味を含んでいますので、未知数の値はいくつになるのかという時に方程式を作って解いて答えを求める作業を行います。
つまり、式=0の時のxやyの未知数の値を求めますので、式=0が成り立つ場合の式を方程式といいます。
小学校の算数の授業は図形の授業が多いですが、中学校の数学の授業は方程式の授業が多くなりますので、方程式がわからなくなったら数学が嫌いになってしまいます。数学の方程式の授業は重要なのです。
そのように嫌いにならない為の方程式の勉強方法は、方程式の構造と解く方法が理解できるようにすることです。一生懸命頑張って勉強を進めてください。
2.1次方程式の構造
この方程式といわれる式には、1次方程式、2次方程式、3次方程式などのいくつかの種類があります。
今回は、いろいろ種類がある方程式の中で1次方程式について説明します。
1次方程式といわれてもどのような式の構造をしているのかわからないですよね。
そこで、1次方程式という言葉を、1次と方程式に分けて考えてみましょう。
- 1次方程式の1次という意味は、未知数の一番大きい次数が1ということです。次数とは何乗かということなので、x、yなどが当てはまります。
- 方程式の意味は、未知数を含んでいる式で、未知数にある値を入れた時に式=0が成り立つ式ということです。
ですので、1次方程式は未知数が1乗を含んでいる式で、1次式=0が成り立つということになります。
また、未知数の数が1つの時は1元、未知数の数が2つの時は2元という言葉が出てくるので覚えてください。
これらをまとめると、1次方程式は下の(1)や(2)のような式のことをいいます。
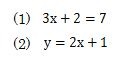
- (1)の式の構造
- 未知数はxが1つなので1元、xは1乗なので1次。
よって、1元1次方程式といいます。解は式=0の時のxの値を求めます。 - (2)の式の構造
- 未知数はxとyで2つあるので2元、xとyは共に1乗なので1次。
よって、2元1次方程式といいます。解は式=0の時のxとyの値を求めます。
1次方程式の式の構造が理解できれば2次方程式の式も理解できます。
1次方程式は、未知数のxとyを扱う基本となる式ですので、しっかり理解しましょう。
