三角形の計算
学習する学年:小学生
1.三角形の面積の説明
三角形とは、3つの頂点とその頂点を結んだ3つの辺でできている図形のことです。
頂点とは、とがった部分の角のことで、辺とは平らな線のことです。
三角形を図形で表すと、下のような形になります。この2つの図形はどちらも3つの角と3つの辺を持った三角形です。
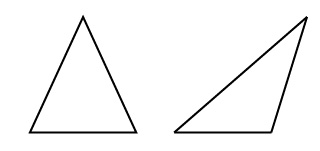
左側の図形は鋭角三角形(えいかくさんかっけい)といって、3つの角が90度より小さい三角形のことです。右側の図形は鈍角三角形(どんかくさんかっけい)といって、1つの角が90度より大きい三角形のことです。
鋭角三角形、鈍角三角形の他には、次のようにいろいろな三角形があります。
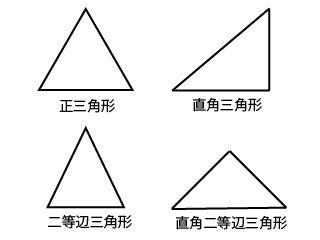
- 正三角形:3つの辺の長さが同じ三角形(3つの角がすべて60°になっている三角形)
- 直角三角形:1つの角が90度になっている三角形
- 二等辺三角形:2つの辺の長さが等しい三角形
- 直角二等辺三角形:1つの角が90度でなおかつ2つの辺の長さが等しい三角形
三角形には上記のような名称があります。三角形の図形と名称はわかりましたでしょうか。
このように、角が3つあり辺が3つある図形を三角形といいます。いろいろな三角形があるので呼び方を忘れないようにしてください。
2.三角形の面積の計算式
三角形の面積を計算する時は、小学校の算数の授業では次の式のように教わりましたよね。
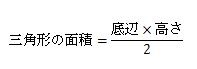
小学校の時は式だけ覚えて計算していましたが、どうしてこのような式になるのか疑問に思いませんか?
- 三角形の面積=(底辺×高さ)÷2
このような式になるには理由があるんです。
理解できるように図形を使って説明していきます。
3.三角形の面積を図形を使って説明
下の三角形の図をみてください。
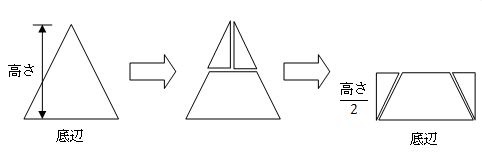
三角形の高さを半分にして切り取った上側の部分を、四角形になるように下半分にはめこみました。
四角形の面積は、縦の長さ×横の長さ、で求められます。
左の図形は三角形だったのに右の図形は四角形になっていますよね。
三角形も高さを半分にすると、縦の長さ×横の長さで面積が求められるということです。
上の図の一番右の図形の縦の長さと横の長さを考えてください。次のようになりませんか。
- 縦の長さ=高さ÷2
- 横の長さ=底辺
したがって、縦の長さと横の長さを計算すると、次のように小学校で教わった(底辺×高さ)÷2という三角形の面積の式になります。
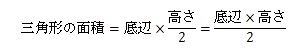
三角形の面積の式の成りたちは理解できたでしょうか。三角形の面積の式=(底辺×高さ)÷2をしっかり覚えてください。
4.三角形の内角の和
三角形の図形のそれぞれの角度について説明します。
三角形の内角の和は180度になります。
※内角とは内側の角度のことです。180°の角度のことを2直角といいます。
どういうことかというと、三角形は3つの角度がありますよね。下の図のような三角形で、a、b、cの角度をすべて足し合わせたら180度になるということです。

正三角形でも直角三角形でもどのような三角形でも内角の和は180度になります。
ちなみに、三角形の外角の和というものもあります。どんな三角形でも外角の和は360度です。
三角形の内角の和を覚えたら何に役に立つのかというと、図形の角度の問題を解く時に役に立ちます。
興味をもった方は、いろいろな角度の三角形を紙に描いて分度器で角度を測って3つを足し合わせると180°になるのか確かめてみてください。
