統計の代表値の平均値、中央値、最頻値の意味と求め方
学習する学年:小学生
1.平均値の意味と求め方
平均値とは、複数のデータを足し合わせて平らにした値のことをいいます。数量データの合計値のちょうど真ん中の値のことです。
また、平均値はデータの分布の中心的な数値として使われる代表値の1つにもなっています。
代表値とは何かというと、平均値、中央値、最頻値の3つの値のことをいいます。統計を勉強すると代表値という言葉はよく出てきますのでしっかり覚えてください。
平均値という言葉は、統計を勉強していなくても、テストの平均点、電気代の平均、体重の平均などを計算する時に普段の生活でも使う頻度が高く誰でも知っているお馴染みの言葉ですよね。
平均値の求め方は、それぞれのデータの値を足し合わせた合計値を、足し合わせるのに使ったデータの個数で割って平均値を計算します。
例えば、
- 5、10、18、24、25、30、32、37、40、50
という10個のデータの値の平均値を求める場合は、
- (5+10+18+24+25+30+32+37+40+50)÷10=27.1
というように、それぞれのデータの合計値÷個数で計算できます。
計算して求めた平均値は、その平均値を基準として個々のデータの値が大きいか小さいかというように、データの傾向を判断する時になくてはならない指標の1つです。
平均値は算数・数学の統計の授業で集団の特徴を調べる他にも、理科の実験で測定した複数のデータの平均を求める時に誤差をなくしてより正確な値にする為にも使われています。
2.中央値の意味と求め方
中央値(メジアン)とは、データを大きさ順に並べた時のちょうど真ん中に当たるデータの値のことをいいます。全データの個数の真ん中の値のことです。
また、中央値はデータの分布の中心的な数値として使われる代表値の1つにもなっています。
※代表値は、中央値、平均値、最頻値の3つの値のことをいいます。
中央値の求め方は、データを大きさ順(小さい順、大きい順)に並べて、そのデータの個数の真ん中を探し出せば中央値が出てきます。
例えば、データの個数が10個あれば、
- (10+1)÷2=5.5
となり、左から5.5番目のデータが中央値です。
データの個数が9個あれば、
- (9+1)÷2=5
となり、左から5番目のデータが中央値です。
中央値の求め方が理解できましたら、次の集団の中央値を求めてみましょう。
- 20、22、24、24、25、25、26、27、30、100
データの個数は10個あり小さい順に並んでいるので左から5.5番目が中央値ですよね。
5.5番目の値は、25と25の間なので、この場合は(25+25)÷2=25というように2つのデータの平均を計算した値が中央値となります。
したがって、25が中央値です。
ここで注意して欲しいことは、中央値と平均値を混同されている方がみえますが全く違うものなのです。
中央値も平均値もどちらも真ん中の値を表しているので同じ意味として使うもののように思えますが、中央値はデータの個数の真ん中、平均値はデータの合計数量の真ん中を表しているという大きな違いがあるので、平均値は外れ値(極端に大きい値や小さい値)があるとその値に引っ張られて大きく影響を受けてしまい、中央値は外れ値の影響は受けにくいという両者異なった特徴を持っています。
では、先ほどの集団の平均値を求めてみると、
- (20+22+24+24+25+25+26+27+30+100)÷10=32.3
となるので、中央値(25)と平均値(32.3)は真ん中の値ですが同じ値にはなりません。
中央値と平均値は同じような値が理想的な分布の形ですが、中央値と平均値は常に同じような値になるとは限りませんので、データの傾向を調べる時は外れ値に左右される平均値と外れ値に左右されない中央値の両方の値を調べることが大切です。
3.最頻値の意味と求め方
最頻値(さいひんち)とは、最も多く出現する値のことをいいます。
また、最頻値はモードともいわれデータの分布の中心的な数値として使われる代表値の1つにもなっています。
※代表値は、最頻値、平均値、中央値の3つの値のことをいいます。
例えば、次の10個のデータの最頻値を求めてみましょう。
- 1、2、3、3、3、3、4、4、5、6
まずは、値ごとにまとめて出現回数をカウントしてください。カウント数は次のようになります。
- 1:1回
- 2:1回
- 3:4回
- 4:2回
- 5:1回
- 6:1回
最頻値とは、最も多く出現する値のことなので、4回出現した3の値が最頻値となります。
棒グラフやヒストグラムなどの統計グラフから最頻値を読み取る時は、一番高い棒や柱の面積が大きい箇所の値を読み取ってください。
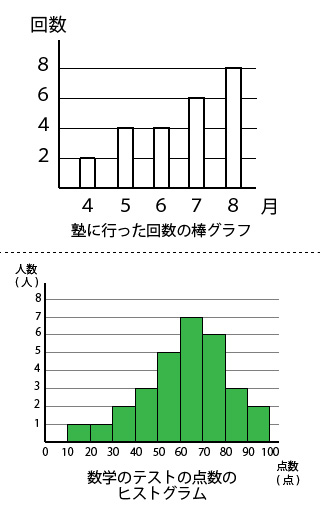
上の2つの統計グラフの最頻値は、棒グラフは8月、ヒストグラムは65点です。
つまり、最頻値とはデータの個数が一番多い値や分類、度数が一番多い階級値(階級の真ん中の値)のことをいいます。
平均値、中央値、最頻値の意味と求め方はわかっていただけたでしょうか?
統計グラフは、平均値、中央値、最頻値も扱わないといけないので忘れないようにしてください。
