帯グラフの描き方の手順
学習する学年:小学生
1.帯グラフの説明
小学校高学年で勉強する統計グラフの種類は、帯グラフ、円グラフ、ドットプロットの3つあります。
帯グラフとは、帯全体を100%の割合として、個々の項目の割合を四角形の面積で表す統計グラフのことです。
データの種類は、ものの種類・区別を表した質的データと数量を表した量的データがありますが、帯グラフは主に質的データを扱うことに適しています。
算数の授業で勉強するグラフは様々あります。そして、個々の項目の割合を表すグラフといえば帯グラフ又は円グラフが一般的です。
帯グラフの特徴は、あくまで帯全体を100%とした時の各項目が占める割合に的を絞ったグラフなので数量イメージがわかりにくいことです。また、全体の数量を使って各項目の割合を算出しないといけず、円グラフよりは見やすいですが多くの項目を帯の中に入れるとグラフが見にくくなってしまうことです。
帯グラフを使う目的は、円グラフと同じように散らばっていた複数のデータが占める割合を比較する為に使います。
帯グラフを描く手順ですが、
- 散らばっているデータをまとめる
- まとめたデータから割合を計算する
- まとめたデータと計算した割合を表にする
- 表の割合の数値を元にして帯グラフを描く
という4工程の順番です。
帯グラフを描くことができたらそれで終わりではなく、描いた帯グラフをじっくり見てグラフからどのような傾向が読み取れるのか考えます。
統計グラフの勉強をして散らばっているデータをまとめてグラフを描き、そして描いたグラフを読み取れる力が身に着くと物事を比較検討する力も同時に身に着きます。
中学生・高校生・大学生・社会人の方で割合(%)の統計グラフの描き方がよくわからないという方は、帯グラフと円グラフを描いて見てください。
以下に帯グラフの描き方を例題を使ってわかりやすく説明していますので描き方を読んでイメージをつかんでください。
2.ある地点の交通量で帯グラフの描き方の例題
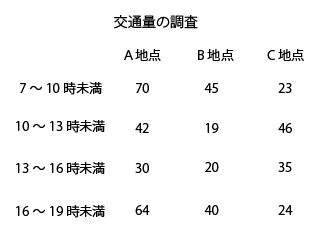
ある日まきちゃんは通学路を歩いていたら危うく車とぶつかりそうになってしまいました。そこで、3地点で時間ごとに車が走行する台数が知りたくなり交通量の調査をして上の図を作りました。
こういう場合を例にして、どのように帯グラフにすればいいのか1つ1つ考えてみましょう。
帯グラフを描く手順は覚えていますか?
1番目は散らばっているデータをまとめる、2番目はまとめたデータから割合を計算する、3番目はまとめたデータと計算した割合を表にする、4番目は表の割合の数値を元にして帯グラフを描くという順番で行ってください。
手順1.
まずは、上の図の交通量の調査結果に書かれているそれぞれの地点の交通量を整理してみましょう。
整理することはとても重要な作業です。みなさんの部屋の中が散らかっているとお母さんにすぐに片付けるように怒られますよね。散らかっていたものをあるべき場所に片付けると綺麗に整理できます。統計も同じで、散らかっているデータを目的に応じて整理すると綺麗になり意味を持つデータに変わります。
この場合は、各地点の時間ごとの交通量の割合を比べるので、地点ごとに時間で整理すれば綺麗にまとまりそうですよね。
上の交通量の調査結果は、A地点、B地点、C地点という順番で時間別に整列させると次のようになります。
- A地点:7~10時未満(70台)、10~13時未満(42台)、13~16時未満(30台)、16~19時未満(64台)
- B地点:7~10時未満(45台)、10~13時未満(19台)、13~16時未満(20台)、16~19時未満(40台)
- C地点:7~10時未満(23台)、10~13時未満(46台)、13~16時未満(35台)、16~19時未満(24台)
ここまでは、今まで勉強してきた絵グラフや棒グラフと同じなので難しくはありませんよね。
手順2.
次は、それぞれの地点の各項目(時間別の交通量の項目)は全体の何%に当たるのかという割合を計算します。
帯グラフは割合を表す統計グラフなので、各項目(時間別の交通量の項目)が占める全体に対する割合が必ず必要となります。
各項目の割合を計算する方法は、各地点の各項目の台数を各地点の交通量全体の台数で割り算してもらえれば求められます。
A地点の交通量の全体の車の台数は、70+42+30+64=206台ですよね。
この206を使って計算してもらうと、
- 7~10時未満:(70÷206)×100=34%
- 10~13時未満:(42÷206)×100=20.4%
- 13~16時未満:(30÷206)×100=14.5%
- 16~19時未満:(64÷206)×100=31.1%
と計算できます。
B地点の交通量の全体の車の台数は、45+19+20+40=124台ですよね。
この124を使って計算してもらうと、
- 7~10時未満:(45÷124)×100=36.3%
- 10~13時未満:(19÷124)×100=15.3%
- 13~16時未満:(20÷124)×100=16.1%
- 16~19時未満:(40÷124)×100=32.3%
と計算できます。
C地点の交通量の全体の車の台数は、23+46+35+24=128台ですよね。
この128を使って計算してもらうと、
- 7~10時未満:(23÷128)×100=18%
- 10~13時未満:(46÷128)×100=36%
- 13~16時未満:(35÷128)×100=27.3%
- 16~19時未満:(24÷128)×100=18.7%
と計算できます。
なお、各項目の割合を足し合わせると100%になるか必ず確認してください。A地点は34+20.4+14.5+31.1=100%、B地点は36.3+15.3+16.1+32.3=100%、C地点は18+36+27.3+18.7=100%となるので正しいです。
これで各地点ごとの各項目の割合の計算が終わりました。
手順3.
次は、まとめたデータと割合を表にしてみましょう。
表を作る時は項目が必要です。この場合は、各地点ごとにある時間で分別して交通量を調べて割合を計算しましたので、地点、時間別の車の台数、そしてそれぞれの割合を項目として表を作るのが適切ですよね。
表を作ると次のようになります。
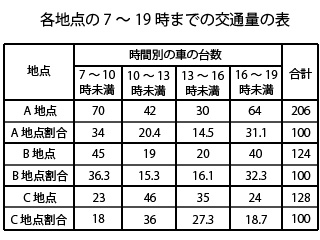
データの整理がしっかりできていれば、表を作ることは難しくないですよね。きれいにまとまりました。
手順4.
最後は、表の割合の数値を元にして帯グラフを描きます。
帯グラフを描く時は、縦軸と横軸の項目と帯の中に複数の項目が必要になります。この場合は、縦軸は地点、横軸は割合として、表の7~10時未満、10~13時未満、13~16時未満、16~19時未満という各項目を使います。
帯グラフを描く時の注意点は、割合は0~100%となるように等間隔で目盛りを書きこんで、各項目はそれぞれの割合に応じた四角形の面積となるように描いて色分けすることです。
したがって、各項目は割合に連動して大きさが変動するということです。項目ごとに色分けができましたら、表から読み取った時間別の車の台数の割合の値をそれぞれの箇所に書いてください。
帯グラフを描くと次のようになります。
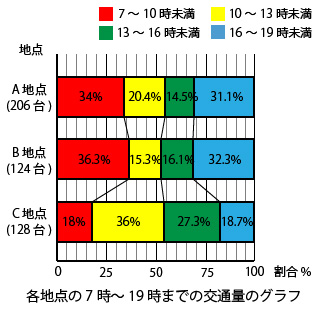
これで帯グラフは完成してすべてのデータの整理が終わりました。
帯グラフが完成した後は、帯グラフからデータの傾向や特徴を考えてみましょう。
まずは、各地点で交通量が多い少ない時間帯の割合を比べて見ると、
- A地点は7~10時と16~19時は交通量が多く、10~16時は交通量が少ない
- B地点は7~10時と16~19時は交通量が多く、10~16時は交通量が少ない
- C地点は10~16時は交通量が多く、7~10時と16~19時は交通量が少ない
ということがわかります。
したがって、A点とB点は朝と夕方に交通量が集中していて、C点は昼間に交通量が集中しているという特徴をつかむことができました。
しかしながら、帯グラフを見ただけでは交通量が何台のなのかわかりませんよね。
棒グラフは数量をそのまま表していましたが、帯グラフは数量ではなく割合を表しているので、全体でどのくらい占めているのかということしかわからないのです。
帯グラフから具体的な数量が知りたい時は、全体の数量と個々の項目の割合を使って数量を計算しないといけないことを覚えておいてください。
例えば、A地点の場合では、
- 7~10時未満:206台×34%=70台
- 10~13時未満:206台×20.4%=42台
- 13~16時未満:206台×14.5%=30台
- 16~19時未満:206台×31.1%=64台
というように数量(台数)は計算できます。
帯グラフは複数の観測点の各項目の割合を比較する時に使うことに適している統計グラフとなります。
帯グラフは個々の割合(%)、棒グラフは数量で使い分けることをわかっていただけたでしょうか。
