ドットプロットの描き方の手順
学習する学年:小学生
1.ドットプロットの説明
小学校高学年で勉強する統計グラフの種類は、ドットプロット、円グラフ、帯グラフの3つあります。
ドットプロットとは、複数のデータをドットの形で積み上げて表す統計グラフのことです。
データの種類は、ものの種類・区別を表した質的データと数量を表した量的データがありますが、ドットプロットはどちらかといえば量的データの連続データを扱うことに適しています。
ドットプロットの特徴は、1つのデータを1つのドットで表し、同じデータが複数ある時はドットを積み上げて表すのでイメージがつかみやすいことです。
ドットプロットを使う目的は、散らばっていた複数のデータの最大値、最小値、最頻値、度数のばらつき方の傾向を調べる為に使います。
ドットプロットを描く手順ですが、
- 散らばっているデータをまとめる
- まとめたデータを表にする
- 表の数値を元にしてドットプロットを描く
の3工程の順番です。
ドットプロットを描くことができたらそれで終わりではなく、描いたドットプロットをじっくり見てグラフからどのような傾向が読み取れるのか考えます。
統計グラフの勉強をして散らばっているデータをまとめてグラフを描き、そして描いたグラフを読み取れる力が身に着くと物事を比較検討する力も同時に身に着きます。
中学生・高校生・大学生・社会人の方で統計グラフの描き方がよくわからないという方は、ドットプロットから勉強するのではなく、まずは絵グラフから描いて見てください。
以下にドットプロットの描き方を例題を使ってわかりやすく説明していますので描き方を読んでイメージをつかんでください。
2.視力検査のデータでドットプロットの描き方の例題
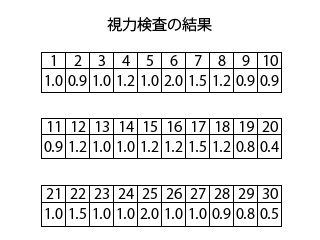
けいこちゃんはメガネをかけなくても視力は1.0あるので目は悪い方ではありません。しかし、けいこちゃんのお友達はメガネをかけているので、自分の視力はクラスの中ではどのくらい良い方なのか知りたくなり、この前行った自分のクラスの視力検査の結果を30人から聞き取り調査してまとめました。
こういう場合を例にして、どのようにドットプロットにすればいいのか1つ1つ考えてみましょう。
ドットプロットを描く手順は覚えていますか?
1番目は散らばっているデータをまとめる、2番目はまとめたデータを表にする、3番目は表の数値を元にしてドットプロットを描くという順番で行ってください。
手順1.
まずは、上の図のバラバラに散らばっている視力をグループごとに分けて整理しましょう。
整理することはとても重要な作業です。みなさんの部屋の中が散らかっているとお母さんにすぐに片付けるように怒られますよね。散らかっていたものをあるべき場所に片付けると綺麗に整理できます。統計も同じで、散らかっているデータを目的に応じて整理すると綺麗になり意味を持つデータに変わります。
視力の種類は、0.1~2.0までありますよね。
したがって、それぞれの視力は視力ごと(0.1~2.0)のグループにして整理すれば綺麗にまとまりそうですよね。
上の図のそれぞれの視力を、0.1、0.2、0.3、0.4・・・1.0、1.2、1.5、2.0ごとに集計してそれぞれ人数を数えると次のようになります。
- 0.1:0人
- 0.2:0人
- 0.3:0人
- 0.4:1人
- 0.5:1人
- 0.6:0人
- 0.7:0人
- 0.8:2人
- 0.9:5人
- 1.0:10人
- 1.2:6人
- 1.5:3人
- 2.0:2人
これで各視力ごとに分けて人数の整理ができました。
手順2.
次は、まとめたデータを表にしてみましょう。
表を作る時は項目が必要です。この場合は、各視力ごとに人数を調べましたので、視力、人数を項目として表を作るのが適切ですよね。
表を作ると次のようになります。
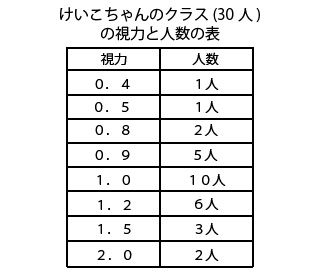
データの整理がしっかりできていれば、表を作ることは難しくないですよね。きれいにまとまりました。
手順3.
最後は、表の数値を元にしてドットプロットを描きます。
ドットプロットは横軸の各値の上方向にドットを積み上げていくグラフなので、ドットプロットを描く時は、横軸の項目が必要になります。この場合は、表の項目の視力を横軸に使えば大丈夫ですよね。
横軸は、一番左が0.1で右に行くほど視力が大きくなるように目盛りを書きこみますが、この場合は0.1~0.3のデータはないので0.4から書きこめばいいです。
横軸の項目と目盛りを書きこみましたら、ドットを横軸の各値の上に縦方向に表から読み取った値を人数分積み上げてください。
※ドットの色は何色でも構いません。
ドットプロットを作ると次のようになります。
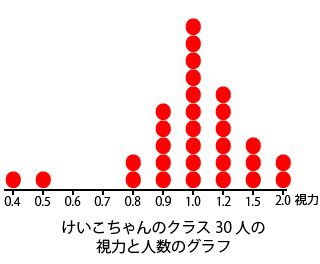
これでドットプロットは完成してすべてのデータの整理が終わりました。
ドットプロットが完成した後は、ドットプロットからデータの傾向や特徴を考えてみましょう。
まずは、クラスの中の視力の最大値と最小値を比べて見ると、
- 一番大きい視力は2.0
- 一番小さい視力は0.4
ということがわかります。
最大値と最小値がわかると範囲(レンジ)が求められます。範囲とは、最大値と最小値の差のことで、この場合は、2.0-0.4=1.6が範囲となります。
範囲が小さいとデータのばらつき方は小さい、範囲が大きいとデータのばらつき方は大きいというように、範囲はデータが全体的にどのようにばらついているのかの目安となります。
次は、人数が一番多い視力(最頻値)を探して見ると、
- 人数が一番多い視力は1.0
ということがわかります。
※一番ドットの数が多かった値のことを最頻値(さいひんち)といい、この場合は視力1.0が最頻値です。
また、視力が0.9~1.2の間に人数が集中していることがわかりますよね。
次は、平均値を計算してみましょう。
平均値とは、全てのデータを足し合わせて合計して、合計するのに使ったデータの個数で割った値のことです。
この場合は、視力ごとの値に人数を掛け合わせて、その計算した値をそれぞれ足し合わせて30で割ってもらうと平均は求められます。
まずは、視力ごとの値に人数を掛け合わせます。
- 0.4×1=0.4
- 0.5×1=0.5
- 0.8×2=1.6
- 0.9×5=4.5
- 1.0×10=10
- 1.2×6=7.2
- 1.5×3=4.5
- 2.0×2=4
次は、それぞれの計算結果を足し合わせて30で割ります。
0.4+0.5+1.6+4.5+10+7.2+4.5+4=32.7
32.7÷30=1.09となるので、平均値は1.09です。
最後は、中央値を計算してみましょう。
中央値とは、複数のデータを大きさ順(小さい順・大きい順)に並べた時の真ん中に位置する値のことです。
この場合は、30人のデータを集計してドットプロットを作ったので、
- (30+1)÷2=15.5
となり、一番小さい視力のデータから大きい方に向かって数えて15番目と16番目の間の値が中央値となります。
したがって、視力が0.4の上に描かれたドットから右方向へ数えて15番目と16番目の値を読んでもらうと1.0が中央値となります。
以上の結果をまとめると、けいこちゃんのクラスの視力の特徴は、0.4~2.0までの間で0.9~1.2に集中していて、1.0を最頻値としてその周辺にばらついていて0.4と0.5は最頻値からかけ離れているという傾向がわかりました。
このように、ドットプロットは、最大値、最小値、最頻値、度数のばらつき方(分布)を比較する時に使うことに適している統計グラフです。
ドットプロットは小学生の高学年で勉強する初歩的なグラフです。スムーズに描くことができるように手順を覚えておいてください。
