ヒストグラム(柱状グラフ)の描き方の手順
学習する学年:中学生
1.ヒストグラムの説明
中学校で勉強する統計グラフの種類は、ヒストグラム(柱状グラフ)があります。
ヒストグラムとは、複数の数量データを階級ごとに集計した度数の分布のばらつき方を調べる統計グラフのことです。
ヒストグラムのことを柱状グラフともいいます。
データの種類は、ものの種類・区別を表した質的データと数量を表した量的データ(離散型、連続型)がありますが、ヒストグラムは量的データ(連続型)を扱うことに適しています。
算数・数学の授業で勉強するグラフは様々あります。統計グラフといえば真っ先にヒストグラムを思い浮かべる人は多いのではないでしょうか。
ヒストグラムの特徴は、連続型の量的データの傾向を調べる時によく使われる統計グラフで、階級ごとにデータを振り分けることで複数の量的データをコンパクトにできることです。
ヒストグラムを使う目的は、広い範囲に数量データが分布している時に階級を使ってコンパクトにグラフに表してデータを分析する為に使います。
ヒストグラムを描く手順ですが、
- 散らばっているデータをまとめる
- まとめたデータを度数分布表にする
- 度数分布表の階級・度数を元にしてヒストグラムを描く
というように絵グラフを描く時と同じ3工程の順番です。
ヒストグラムを描くことができたらそれで終わりではなく、描いたヒストグラムをじっくり見てグラフからどのような傾向が読み取れるのか考えます。
統計グラフの勉強をして散らばっているデータをまとめてグラフを描き、そして描いたグラフを読み取れる力が身に着くと物事を比較検討する力も同時に身に着きます。
中学生・高校生・大学生・社会人の方で統計グラフの描き方がよくわからないという方は、ヒストグラムではなく絵グラフから描いて見てください。
以下にヒストグラムの描き方を例題を使ってわかりやすく説明していますので描き方を読んでイメージをつかんでください。
2.数学のテストの点数でヒストグラムの描き方の例題
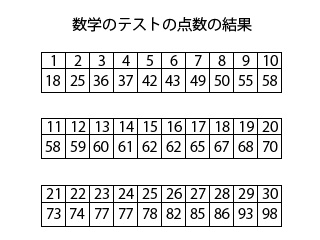
まさし君は全く勉強をせずに数学のテストを受けたら18点というクラスの中で一番最低な点数を取ってしまいお母さんからこっぴどく叱られてしまいました。そこで、クラスのみんなは何点取っているのか知りたくなり、クラス30人から数学のテストの点数を聞いて上の図のようなテストの点数が低い順にまとめたメモを作りました。
こういう場合を例にして、どのようにヒストグラムにすればいいのか1つ1つ考えてみましょう。
ヒストグラムを描く手順は覚えていますか?
1番目は散らばっているデータをまとめる、2番目はまとめたデータを度数分布表にする、3番目は度数分布表の階級・度数を元にしてヒストグラムを描くという順番で行ってください。
手順1.
まずは、上の図の数学のテストの点数のメモに書かれているそれぞれの点数を整理してみましょう。
統計グラフを描く時はデータを整理することはとても重要な作業です。散らかっているデータは目的に応じて整理することで意味を持つデータに変わり、データの整理の良し悪しで統計グラフの質に大きく関係してきますので、面倒くさがらずにしっかり整理してください。
ヒストグラムは他の統計グラフと明らかに違うところは階級を決めなければいけないことです。階級とはデータの区間のことで、それぞれの区間ごとにデータを集計してその集計した値(度数)を使ってグラフを描きます。
この場合は、0~100点までのテストの点数を比べるので、階級の幅を10点刻みで整理すれば綺麗にまとまりそうですよね。
上の数学のテストの点数は、0点以上~10点未満、10点以上~20点未満・・・80点以上~90点未満、90点以上~100点という各階級で整列させてみると次のようになります。
- 0点以上~10点未満:なし
- 10点以上~20点未満:18点
- 20点以上~30点未満:25点
- 30点以上~40点未満:36点、37点
- 40点以上~50点未満:42点、43点、49点
- 50点以上~60点未満:50点、55点、58点、58点、59点
- 60点以上~70点未満:60点、61点、62点、62点、65点、67点、68点
- 70点以上~80点未満:70点、73点、74点、77点、77点、78点
- 80点以上~90点未満:82点、85点、86点
- 90点以上~100点:93点、98点
これで階級ごとに点数を分けて整理ができました。
手順2.
次は、まとめたデータを度数分布表にしてみましょう。
度数分布表を作る時は、階級と度数が必要です。この場合は、点数を階級、人数を度数として度数分布表を作るのが適切ですよね。
各階級の点数はそのまま使うのではなく、いくつあるのかカウントすることでカウント数が度数(人数)となります。
度数分布表を作ると次のようになります。

データの整理がしっかりできていれば、度数分布表を作ることは難しくないですよね。きれいにまとまりました。
手順3.
最後は、度数分布表の階級と度数を元にしてヒストグラムを描きます。
ヒストグラムを描く時は、縦軸は度数、横軸は階級として描くルールがあります。
縦軸は、一番下が0で上に行くほど度数が増えるように目盛りを書きこみます。横軸は、左から右に向かって大きくなるように階級幅を書きこみます。
縦軸と横軸に階級・度数の項目と目盛りを書きこみましたら、横軸の上に縦方向に度数分布表から読み取った度数の値を柱の形で描いてください。
※縦軸は度数、横軸は階級、横軸の上に度数に応じた長さの柱を描く、柱と柱の間は空間を空けないように描くということを必ず守ってください。
ヒストグラムを描くと次のようになります。
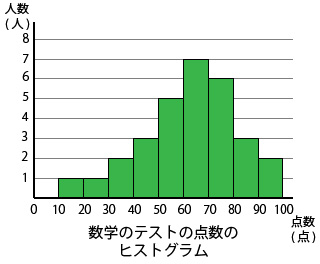
これでヒストグラムは完成してすべてのデータの整理が終わりました。
ヒストグラムが完成した後は、ヒストグラムからデータの傾向や特徴を考えてみましょう。
まずは、階級の大きい小さいを比べて見ると、
- 階級が一番大きいのは90~100の階級
- 階級が一番小さいのは10~20未満の階級
ということがわかります。
次は、度数が多い少ないを比べて見ると、
- 度数が一番多いのは60~70未満の階級
- 度数が一番少ないのは10~20未満と20~30未満の階級
ということがわかります。
したがって、まさし君のクラス30人の数学のテストの点数の特徴は、10点~100点までばらついていますが、60~70点未満の人が特に多いことがわかりました。
ヒストグラムは柱の面積の大小で度数を表す統計グラフなので、柱の面積を見ればどの辺りにデータが集中しているのかばらついているのかがはっきりわかります。
ヒストグラムは棒グラフととても似ているグラフですが、全く違う特徴を持っているので間違えないようにしてください。
ヒストグラムと棒グラフの違いは何かというと、ヒストグラムの縦軸はデータの起こりやすさを表しているのに対して、棒グラフの縦軸は個々のデータの値を表していることです。
また、ヒストグラムは連続型の量的データ(小数点を含むデータ)を扱うのに適しているので柱と柱の間はくっついているのに対して、棒グラフは質的データや離散型の量的データ(整数のみのデータ)を扱うのに適しているので棒と棒の間が空いているという違いがあります。
このように、連続しているデータの時はヒストグラム、連続していないデータの時は棒グラフというように、連続しているか連続していないかでグラフを使い分けてデータの傾向をつかんでください。
ヒストグラムは、複数の数量データを階級ごとに分けて集計してコンパクトにすることで、全体の度数のばらつき方の傾向を見やすくする時に使うことに適している統計グラフです。
棒グラフとヒストグラムはグラフの雰囲気が似ていても全くの別物のグラフということがわかっていただけたでしょうか。
