散布図の描き方の手順
学習する学年:高校生
1.散布図の説明
高校で勉強する統計グラフの種類は、散布図、箱ひげ図の2つあります。
散布図とは、縦軸と横軸の項目の関係性を表す統計グラフのことです。
データの種類は、ものの種類・区別を表した質的データと数量を表した量的データがありますが、散布図はどちらのデータでも扱うことはできます。
散布図は関係性を調べるのに特化した特徴を持ったグラフなので、散布図を使う目的は2つのものの関係が正の相関関係なのか負の相関関係なのかの傾向を調べる為です。
散布図を描く手順ですが、
- 散らばっているデータをまとめる
- まとめたデータを表にする
- 表の数値を元にして散布図を描く
の3工程の順番です。
散布図を描くことができたらそれで終わりではなく、描いた散布図をじっくり見てグラフからどのような傾向が読み取れるのか考えます。
統計グラフの勉強をして散らばっているデータをまとめてグラフを描き、そして描いたグラフを読み取れる力が身に着くと物事を比較検討する力も同時に身に着きます。
中学生・高校生・大学生・社会人の方で統計グラフの描き方がよくわからないという方は、散布図から勉強するのではなく、統計グラフの基本である絵グラフから描いて見てください。
以下に散布図の描き方を例題を使ってわかりやすく説明していますので描き方を読んでイメージをつかんでください。
2.世帯別の電気代で散布図の描き方の例題
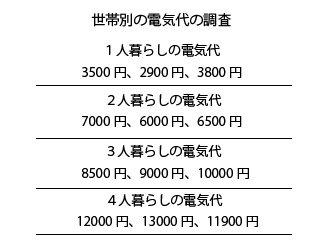
しょうた君は世帯の人数と電気代の間には何かしらの関係性はないのか調べる為に、1人暮らし、2人暮らし、3人暮らし、4人暮らしをしている世帯の電気代を各3組から聞き取り調査しました。上の図はその時に作った世代別の電気代のメモです。
こういう場合を例にして、どのように散布図にすればいいのか1つ1つ考えてみましょう。
散布図を描く手順は覚えていますか?
1番目は散らばっているデータをまとめる、2番目はまとめたデータを表にする、3番目は表の数値を元にして散布図を描くという順番で行ってください。
手順1.
まずは、上の図の電気代をグループごとに分けて整理しましょう。
統計グラフを描く時はデータを整理することはとても重要な作業です。散らかっているデータは目的に応じて整理することで意味を持つデータに変わり、データの整理の良し悪しで統計グラフの質に大きく関係してきますので、面倒くさがらずにしっかり整理してください。
この場合のグループは世帯別(1人暮らし、2人暮らし、3人暮らし、4人暮らし)が適していますよね。
したがって、それぞれの世帯ごとのグループにして電気代を整理すれば綺麗にまとまりそうです。上の図は世帯ごとに電気代を整理してメモを作っていますが、1人暮らし、2人暮らし、3人暮らし、4人暮らしに分けて電気代のデータをもう一度まとめてみます。
- 1人暮らし:3500円、2900円、3800円
- 2人暮らし:7000円、6000円、6500円
- 3人暮らし:8500円、9000円、10000円
- 4人暮らし:12000円、13000円、11900円
これで世帯ごとに分けた電気代の整理ができました。
手順2.
次は、まとめたデータを表にしてみましょう。
表を作る時は項目が必要です。この場合は、各世帯ごとの電気代を調べましたので、世帯、電気代を項目として表を作るのが適切ですよね。
表を作ると次のようになります。
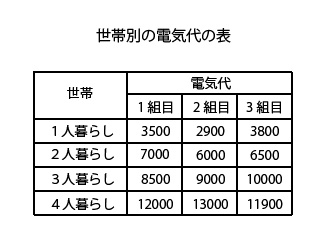
データの整理がしっかりできていれば、表を作ることは難しくないですよね。きれいにまとまりました。
手順3.
最後は、表の数値を元にして散布図を描きます。
散布図はデータの値が縦軸と横軸で交差した所で点をプロットして、点の並び方で相関関係を調べるグラフなので、散布図を描く時は縦軸と横軸の項目が必要になります。この場合は、表の項目の電気代を縦軸、世帯を横軸に使えば大丈夫ですよね。
縦軸は、一番下が0で上に行くほど電気代が高くなるように目盛りを書きこみます。横軸は、左から右に向かって1人暮らし、2人暮らし、3人暮らし、4人暮らしというように分類を書きこみます。
縦軸と横軸の項目と目盛り・分類を書きこみましたら、表から読み取った値を点としてグラフにプロットしてください。
※点の色は何色でも構いません。
散布図を作ると次のようになります。
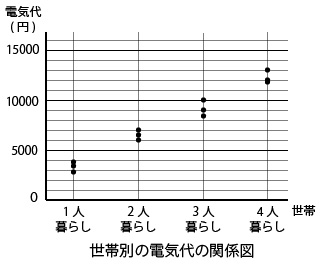
これで散布図は完成してすべてのデータの整理が終わりました。
散布図が完成した後は、散布図からデータの傾向や特徴を考えてみましょう。
まずは、散布図で電気代の最大値と最小値を比べて見ると、
- 電気代が一番高いのは4人暮らしの13000円
- 電気代が一番安いのは1人暮らしの2900円
ということがわかります。
統計グラフから最大値と最小値を探し出して比べるだけならば棒グラフでもできますよね。
散布図のいいところは、グラフにプロットした点の並び方で縦軸と横軸の相関関係が調べられることなので、次は相関関係を調べてみましょう。
相関関係とは、2つのものの間にある関係性(ある項目とある項目の関係性)のことです。
散布図を描くとわかることは、左下から右上方向に向かって点が集まっていれば正の相関関係、左上から右下方向に向かって点が集まっていれば負の相関関係があるということです。
右上がりで点が並んでいるか右下がりで点が並んでいれば相関関係があります。全体に点が散らばっていれば相関関係はありません。
したがって、この場合は電気代と世帯の関係性がわかります。点が右上がりで並んでいれば正の相関関係、点が右下がりで並んでいれば負の相関関係があるので、上のグラフは左下の位置から右上に向かってデータの点が並んでいるので、世帯別の電気代は正の相関関係があるということがわかりますよね。
以上の結果をまとめると、上のグラフから言えることは、世帯の人数が多くなれば電気代は高くなるという傾向があるということです。
このように、散布図は相関関係(正の相関、負の相関)を調べる時に使うことに適している統計グラフです。
