直方体の計算
学習する学年:小学生
1.直方体の説明
直方体(ちょくほうたい)とは、すべての面が長方形で成り立っていたり、長方形と正方形で成り立っている6面体のことです。
直方体を図形で表すと、下の図のような形になります。
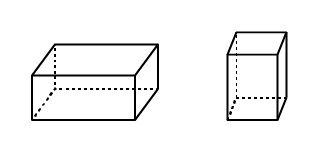
この図形をみてもらえればわかると思いますが、すべての面が長方形で構成されています。
また、直方体の特徴としては、頂点の数は8つ、辺の数は12本あります。
では、下の図形はどうでしょか?
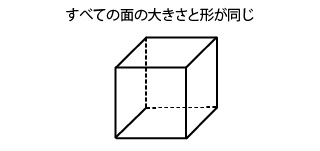
この図形は、頂点の数は8つ、辺の数は12本あるので直方体ですね。しかしながら、すべての面が同じ大きさで同じ形の正方形で構成されています。
そのような同じ正方形が6個組み合わされた図形は立方体(りっぽうたい)、別の名称では、正六面体(せいろくめんたい)といい、一般的に立方体は直方体に含まれますので覚えておいてください。
2.直方体の体積の求め方
直方体がどのような形をしているのか解かったところで、次は直方体の体積を求めてみましょう。
体積とは、図形の中の空間や数量を表したもので、縦×横×高さで求めることができます。
下の直方体の図形を使って説明します。
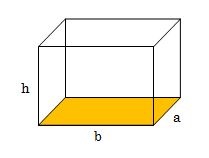
直方体の体積を求める時は、次の式を使って計算してください。
- 直方体の体積=底面の縦の長さ×底面の横の長さ×高さ
つまり、直方体の体積=底面積×高さ、という式を使ってもらえれば答えを導くことができます。
底面積と高さを計算する時は、
- 底面積(図形の黄色の面積)=a×b
- 高さ=h
になります。
したがって、
- 直方体の体積=abh
となります。
3.直方体の体積の計算
最後に直方体の体積を実際に計算してみましょう。
この直方体の体積を求めてみます。
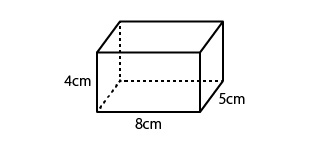
この立方体のそれぞれの辺の長さは、a=5cm、b=8cm、h=4cmです。
この数字を直方体の体積を求める式に当てはめてみましょう。
直方体の体積=底面積×高さ=5cm×8cm×4cm=160cm3となります。
cm3のことを立方センチメートル、m3のことを立方メートルといい体積を求める時の単位として使います。
なお、体積と表面積を混同されている方がいますが違うものなので注意してください。体積は図形の中身の大きさのことでしたが、表面積とは図形の表面の面積のことです。
つまり、次のように立体の図形を切り開いて展開図にすれば表面積はわかります。
上の図形のような斜め上から見た図を見取り図、下の図形のような平面にした図を展開図といいます。
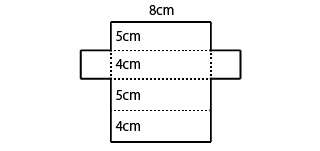
上の図形で計算すると、(8×5)×2+(8×4)×2+(5×4)×2=184cm2となります。
直方体の体積の計算は、それぞれの辺の長さを掛け合わせれば答えが求まりますので簡単だったと思います。
