数学の連立1次方程式を代入法を使って解く方法

学習する学年：中学生

１．連立1次方程式を代入法で解く方法

連立1次方程式は中学校の数学では重要なところです。連立1次方程式の解き方がわからないと数学が嫌いになってしまいますので解き方をしっかり覚えてください。

連立1次方程式の解き方には、代入法と加減法の2つの方法があります。

代入法と加減法のどちらを使っても連立1次方程式の答えを導き出す事はできますが、どちらが簡単な方法かと言うと代入法です。

今回は簡単な代入法について説明しますので、加減法で解く方法を勉強したい方は、こちら 連立1次方程式の解法2 をご覧ください。

連立1次方程式を代入法で計算する時のポイントは次の3つです。

• 2つある式のどちらかの式を移項を使って、x＝、又はy＝の形に変えてください。
• x＝、又はy＝の式に変えましたら、移項をしなかった式にそのxかyの値を代入してください。
• x＝、又はy＝の答えを求めましたら、どちらかの式に答えを代入してもう1つの答えを求めてください。

この3つの作業をすることにより答えにたどり着きます。計算方法は単純なので1回計算してもらうと理解できると思います。

移項がよくわからないという方は、こちら 倍分、変形、移項 を見て勉強してください。

２．連立1次方程式を代入法を使って解いてみよう

それでは、次の連立1次方程式を代入法を使って解いてみましょう。

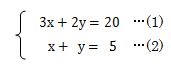
上記で説明した連立1次方程式を代入法で計算するポイントの通りに計算してください。

まず初めは、式をx＝かy＝にしなければなりませんよね。

上の式の（1）でも（2）でもどちらでも構いませんが、x＝、又はy＝の式に移項して変形します。

式をよく見ると式（2）の方が変形しやすいと思いますので、式（2）をy＝にしてみると式（3）のようになります。

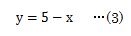
式（3）のようにy＝に変形しましたら、式（3）を式（1）のyに代入します。

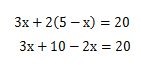
3x＋10－2x＝20になるので、左辺の10を右辺へ移項してxの値を求めます。

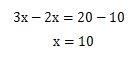
連立1次方程式を代入法で計算するポイントの通りに計算すると、x＝10という答えが出ました。

ここまで計算すれば後は簡単です。

次は、このx＝10を式（1）か式（2）に代入してyの値を計算します。

式を見ると式（2）の方が簡単そうに思いますので式（2）に代入します。

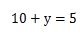
代入すると10＋y＝5となるので、左辺の10を右辺へ移項してyの値を求めます。

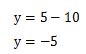
計算するとy＝－5という答えが出ました。

したがって、答えは、x＝10、y＝－5となります。

最後に、答えが本当に正しいか確認してみましょう。

答えが正しいのか確認する方法は、x＝10、y＝－5を、式(1)と式（2）に代入して式が成り立つのか確かめてください。

答えを式（1）に代入した場合は次のようになります。

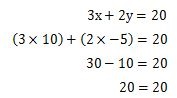
答えを式（2）に代入した場合は次のようになります。

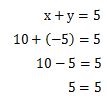
それぞれの式（1）と式（2）の左辺と右辺の値が等しくなりました。

値が同じになったことが確認できましたので、答えは正しかったことがわかりました。