1次関数(方程式)のグラフ
学習する学年:中学生
1.1次関数(1次方程式)のグラフの描き方
1次関数(方程式)のグラフの描き方はわかりますか?
1次関数のグラフの描き方を考えてみましょう。
1次関数のグラフを描く時は、次の作業を行ってください。
- 座標軸といわれるx軸とy軸を直交させて線を引き座標平面を用意します。
- 座標平面上では、x軸、y軸に対応させる座標として、xの値とyの値を実数で用意して点として描きます。
- 座標平面上に点を描いたら点と点を線で結びます。
※座標平面とは縦横に線を引いた方眼用紙のことです。
ですので、1次関数のグラフを描く時は、座標平面(x軸、y軸)と点の位置の座標が必要です。
例えば、y=3x+1という1次式を使ってグラフを描いてみましょう。
yがxの関数であれば、xに対するyの値は決まっているので、xとyの値を使ってグラフを描くことができます。
なお、グラフとは関数(方程式)を満たす点の集合のことです。
このy=3x+1の式をグラフに描くと下のグラフのようになります。
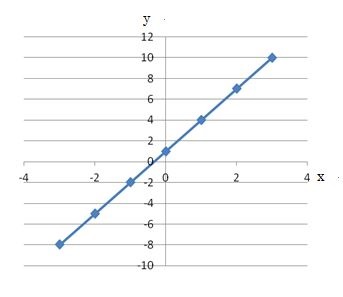
このように、座標平面上に座標から読み取った点を打ったら点と点を線で結ぶと1次関数のグラフとなります。
2.1次関数(1次方程式)のグラフを増減表と1次式の傾き・切片から描く
1次関数(1次方程式)のグラフを描く方法は次のように2つあります。
- 増減表を作ってグラフを作る。
- 1次式から傾きと切片を読み取ってグラフを作る。
どちらの方法でもグラフを描くことができますが、まずは増減表を作ってグラフを描きましょう。
y=3x+1の式のx=-3~3までの値をxに代入してyの値を求めてください。
増減表を作ると次のようになります。

x=-3、-2、-1、0、1、2、3の時のyの値を求めましたら、その値をグラフに点をプロットして点を線で結べばグラフは描けれます。
増減表を作って求めた(x,y)=(-3,-8)、(-2,-5)、(-1,-2)、(0,1)、(1,4)、(2,7)、(3,10)を座標として座標平面に点を打って点を通るように線を引いてください。グラフを描くと上のグラフが描けれます。
次は、1次式から値を読み取ってグラフを描く方法を説明します。
式から値を読み取る時は傾きと切片を求めます。傾きとは係数のこと、切片とは定数項のことなので次の値を読み取ってください。
- 傾き=係数
- 切片=定数項
では、y=3x+1の式の傾きと切片を見てみましょう。

この式の場合は、係数は傾きなので、傾き=3、定数項は切片なので、切片=1になります。
傾きと切片はどのように使えばいいのかというと次のような関係があります。
- 傾きとはxが+1移動した時にyがどれだけ移動するかの値
- 切片とはxが0の時のyの値(直線がy軸と交わるy座標のこと)
傾きとはxが1の時のyの値なので、x=1の時y=3になりますが、yの切片=1なのでyの値は3+1=4になります。したがって、x=1、y=4になります。
切片とはxが0の時のyの値のことです。切片=1なので、x=0、y=1となります。
この2点(x,y)=(0,1)、(1,4)をプロットして直線を引けば上記と同じグラフが描けます。
なお、傾きが0より大きい時は右上がりの直線、0より小さい時は右下がりの直線になります。
3.1次関数(1次方程式)の反比例のグラフを描く
最後に、1次関数の式の反比例の時の関係を見てみましょう。
次の式はxが分母にありますよね。
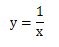
このような反比例の式は直線のグラフにはなりません。
xとyの値の増減表を作ってグラフを描いてみましょう。
増減表
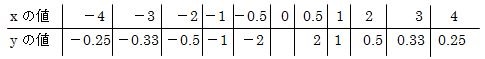
グラフ
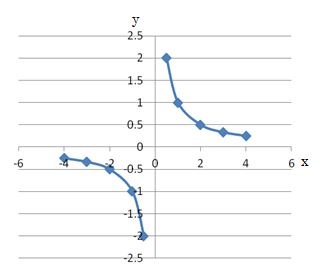
分数の計算は、分母、分子にゼロを入れたらダメなので、x=0の時のyの値はありません。不思議なグラフになりました。
関数はxとyの値を座標にしてグラフに点をプロットすれば関数のグラフが作れますので、グラフを描いてみてxとyの値の変化を確認してみてください。
1次関数(方程式)のグラフの描き方は理解できたでしょうか。
次は、2次関数(方程式)のグラフについてみていきましょう。
