数学の弧度法（ラジアン法）の説明

学習する学年：高校生

１．角度を表す単位

みなさんは、角度を表す単位といえば真っ先に思いつくものは何ですか？

角度を測る単位として、小学生、中学生で勉強してきたことは度数法（どすうほう）ですよね。小学生の時は、分度器を図形の角に当てて何度あるか測っていたと思います。

度数法を使えば次のように角度が求まりますよね。

• 円を4分の1にすれば90°
• 円を半分にすれば180°
• 円を1周すると360°

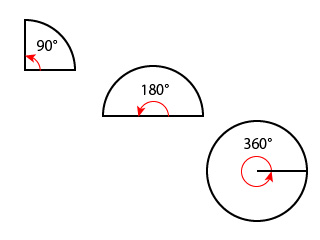
このように、度数法では度数表示の記号である度（°）を使ってきました。

この親しんできた度数法の他に、高校生からは弧度法（こどほう）という角度の表し方を習い始めます。

角度の表し方には、小学校で勉強する度数法と高校で勉強する弧度法の2つの表し方があるので覚えてください。

２．弧度法の説明

弧度法とは何かというと、円を1周すると2π（rad）とする測り方のことです。

radはラジアンと読み弧度法の単位のことを表しています。2π（rad）は2パイラジアンと読みます。

また、弧度法はラジアン法とも呼ばれていて、弧度法（ラジアン）は次のように定義されています。

円において半径と同じ長さの孤に対する中心角を1（rad）とする。

つまり、円周の長さは2πrなのでrを1として長さに関係なく計算すると、2π（rad）＝6.28（rad）＝360°となり、1（rad）＝180°／π≒57.3°ということです。

したがって、弧度法は角度を円周の長さに置き換えて表現する方法のことで、度数法で360°、180°、90°と表していたものは、弧度法では円の半径rの長さに関わらずに次のように表現できるようになります。

• 360°＝2π（rad）
• 180°＝π（rad）
• 90°＝2分の1π（rad）

頭がパニックになってきたと思いますがよく使うことがあるので弧度法の仕組みを覚えてください。

角度を表す時は、度数法でも弧度法でもどちらの方法を使っても間違えではありませんが、学問によっては弧度法を使ったり、与えられている問題の内容によっては弧度法で答えないとマルをもらえないことがありますので、どちらの角度の表示方法が適切なのかを判断して使い分けてください。

３．角度の変換方法

弧度法って面倒な表示方法だなと思われた方がいると思いますが、ちゃんと度数（°）からラジアン（rad）へ、ラジアン（rad）から度数（°）へ変換する式がありますので安心してください。

それでは、度数からラジアンへの変換式、ラジアンから度数への変換式、度数とラジアンの関係について紹介しますので、勉強の参考にしてください。

度数（°）からラジアン（rad）への変換式

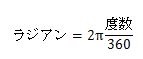
ラジアン（rad）から度数（°）への変換式

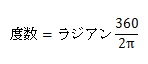
例えば、度数が180°の時、ラジアン（rad）に変換してみると、

• 2π×（180/360）＝π（rad）

となります。

例えば、ラジアンが2π（rad）の時、度数（°）に変換してみると、

• 2π×（360/2π）＝360°

となります。

度数とラジアンの関係は次の表のようになります。

度数とラジアンの関係

度（°）	0	30	45	60	90	180	270	360
ラジアン（rad）	0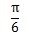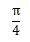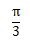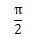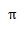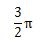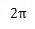

弧度法の表示は少しやっかいですが、高校生や大学生の数学の授業ででてきますし、工業高校や理数系の大学では数学以外の授業でも当たり前にでてきますので覚えましょう。