数学で使う指数の説明

学習する学年：中学生

１．指数の説明

指数とは、数を何乗しているのかということを、ある数の右肩に表している数字のことです。

何乗という言葉を使わなくて説明すると、ある数を何回掛け合わせているのかということを表しています。

下の指数を見てください。

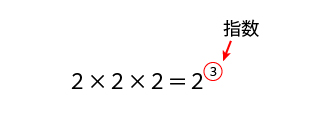
2³（にのさんじょう）と書かれています。2³ですので、ある数が2で、指数が3になります。

• ある数：2
• 指数：3

したがって、2を2×2×2で3回掛け合わせてもらうと、2³として表すことができます。

では、次の数の指数はいくつになるのか考えてみましょう。

例えば、

• 3×3＝

という計算式があるとします。

この式は、3という数を連続して2回掛け合わせることを意味しています。

したがって、3×3＝3²（さんのにじょう、さんのじじょう）なので指数は2です。

3×3の式を3²として表すと式を短くして数を表現できますよね。

このように、同じ数を連続して掛け合わせる時は指数という方法を使うと式を短くして表現することができます。

では、次の式の指数はいくつでしょうか。

• 3×3×3×3×3＝

計算式を指数を使って表して見ると、3を連続して5回掛け合わせています。

したがって、3⁵とすることができますので指数は5です。

なお、指数を計算する時は次のような便利な法則がありますので、計算する時は参考にしてください。

※aは底、mとnは指数といいます。aは0より大きい数、mとnは整数であれば法則は成り立ちます。

それでは、指数に慣れるためにいろいろ計算してみましょう。

２．指数の計算

１．次の数の指数はいくつでしょうか？

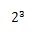
この数は2の3乗といいます。指数とは何乗の部分ですので、指数は3です。

２．次の数の指数はいくつでしょう？

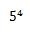
この数は5の4乗といいます。指数とは何乗の部分ですので、指数は4です。

３．次の数の指数はいくつでしょう？

この数は-17の6乗といいます。指数とは何乗の部分ですので、指数は6です。

４．次の数の指数はいくつでしょう？

この数は99の-10乗といいます。指数とは何乗の部分ですので、指数は-10です。

指数のことが少しわかってきたと思いますので、次の指数を使って計算して数を求めてみましょう。

５．次の指数を含んだ数を計算してください。

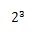
これは、2を連続して3回掛け合わせるということです。

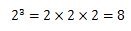
６．次の指数を含んだ数を計算してください。

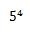
これは、5を連続して4回掛け合わせるということです。

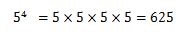
７．次の指数を含んだ数を計算してください。

• -5⁴=

これは、-5を連続して4回掛け合わせるということです。

• -5×-5×-5×-5=625

したがって、-5⁴=625

８．次の指数を含んだ数を計算してください。

• 2³×2⁴=

上で紹介した法則を使って計算してみると、

• 2³×2⁴=2^3＋4=2⁷

となります。

したがって、2⁷=128

９．次の指数を含んだ数を計算してください。

• 2⁰=

上で紹介した法則を使って計算してみると、

• 2⁰=1

となります。

ちなみに、3⁰、4⁰、10⁰でも1になります。

10．最後に、次の指数を含んだ数を計算してください。

• 2^-3=

上で紹介した法則を使って計算してみると、

• 2^-3=1/2³

となります。

したがって、1/2³=1/8

３．指数が分数（有理数）の場合

中学生では指数が分数（有理数）になっている計算は出てきませんが、高校生になると指数が分数（有理数）になっている計算が出てくるようになります。

例えば、2^1/2は、

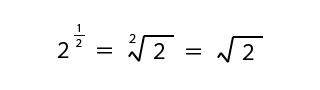
というように2の2乗根（平方根）となります。

例えば、2^5/3は、

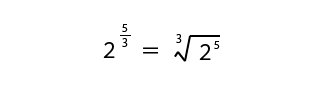
というように2の5乗の3乗根（立法根）となります。
※平方根とは2乗根、立法根とは3乗根のことです。平方根、立方根などのことを累乗根といいます。

指数が分数（有理数）になっている時は、次のような法則がありますので計算する時は参考にしてください。

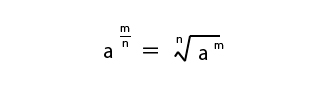
※aは0より大きい数、mは整数、nは正の整数の時に成り立ちます。

指数の計算は特に難しくなかったと思います。指数を含んだ数を計算する時の基本は、指数の個数だけ底を掛け合わせることです。

指数が分数（有理数）になっていたらルート（2乗根、3乗根・・・）として表すことができるということです。