倍数・公倍数の説明と求め方
学習する学年:小学生
1.倍数の説明
みなさんは、倍数(ばいすう)という言葉は、学生時代の算数・数学の授業でしつこいくらい聞いていて、教科書にも2の倍数、5の倍数などとちょくちょく出てきていたので意味はわかっているのではないでしょうか。
倍数とは、整数 a が整数 b の整数倍であり、a を b で割ったときに割り切れるのであれば、a を b の倍数といいます。
算数が苦手の方は、a、bがどうのこうの言われても頭がちんぷんかんぷんになりこんがらがると思うのでもっと簡単にまとめると次のようになります。
倍数は、ある整数を何倍かした数のことを表しています。そのように覚えておけばいいでしょう。
では、どういう数が倍数といえるのかというと、2の倍数、3の倍数、4の倍数、5の倍数などいくつでもあります。
次の倍数の例題を使って具体的に考えていきましょう。
2.3の倍数はいくつ?(倍数の例題1)
それでは、倍数について勉強していきましょう。倍数を勉強する前に九九を覚えていた方がのみ込みが早いので、九九がわからない方は九九を勉強してください。
例えば、ある整数を3として倍数を求めてみましょう。
上記の説明の通り、倍数とは、ある整数を何倍かした数のことですので、この場合は、3という数を1から順番に掛け合わせていくことで倍数が求まります。
3の数を1から順番に掛け合わせていくと次のようになります。
- 3×1=3
- 3×2=6
- 3×3=9
- 3×4=12
- 3×5=15
- 3×6=18
この先も、3×7=21、3×8=24のようにずっと掛け算が続きますが省略します。
よって、3の倍数とは、3、6、9、12、15、18・・・という数のことを表しています。
※3×0=0も倍数に含まれますが省略することが普通です。
この数字の並びのパターンは九九の勉強で見覚えがありませんか。実は、九九の3の段そのものです。
倍数とは、ある数を1倍、2倍、3倍というように整数倍した数のことなので、九九がわかっていれば無意識のうちに倍数を計算していたということです。
3.2の倍数はいくつ?(倍数の例題2)
倍数の求め方は、上記の例題1を解いてみて理解できたでしょうか?
もう1つ例題として、2の倍数を見ていきましょう。2の場合も1から順番に掛け合わせていくだけなので九九がわかれば簡単に求められます。
2の数を1から順番に掛け合わせていくと次のようになります。
- 2×1=2
- 2×2=4
- 2×3=6
- 2×4=8
- 2×5=10
- 2×6=12
この先もずっと掛け算が続きますが省略します。
よって、2の倍数は、2、4、6、8、10、12・・・となります。
※2×0=0も倍数に含まれますが省略することが普通です。
このように、倍数は、ある整数を1から順番に掛け合わせていくと求められるようになります。九九がわかれば倍数の計算は難しくないことがわかっていただけたでしょうか。
4.公倍数の説明
公倍数(こうばいすう)という言葉はあまり聞きなれないですね。倍数は知っていても公倍数は知らないという方や勉強していたとしても忘れている方が多いのではないでしょうか。
公倍数とは、2つ以上の整数に共通な倍数のことをいいます。
倍数と公倍数はどこが違うのかというと、倍数は1つの整数に対して行っていましたが、公倍数では2つ以上の整数に対して行います。
また、公倍数と公約数は同じような漢字なのでどちらも同じものだと勘違いしている方がみえますが違うので気をつけてください。
それでは、どういう数が公倍数といえるのか、次の例題を使って具体的に考えていきましょう。
5.2と3の公倍数はいくつ?(公倍数の例題1)
上記の倍数の例題1の3の倍数と例題2の2の倍数を使って、2と3の公倍数を求めてみましょう。
公倍数を求めるには手順があるので次の様に作業を進めてください。
公倍数を求める時の手順は次の通りです。
- 初めは、それぞれの数の倍数を書き出します。
- 次は、倍数を書き出したら共通の倍数を探します。
それでは、公倍数の求め方がわかりましたら、初めの作業は、2の倍数と3の倍数を書き出してみましょう。
2の倍数は、
- 2、4、6、8、10、12・・・
となります。
3の倍数は、
- 3、6、9、12、15、18・・・
となります。
次の作業は、2の倍数と3の倍数に共通な倍数を探します。
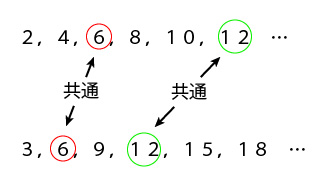
共通とは、どちらにも当てはまる数のことです。2の倍数(2、4、6、8、10、12・・・)と3の倍数(3、6、9、12、15、18・・・)、この2つの数の倍数のどちらにも含まれている倍数を探し出せば、その倍数が共通の倍数ということです。
それぞれの倍数を見ると、6、12・・・が共通になっていますね。
したがって、2と3の公倍数は、6、12・・・になります。
この例題では、2つの整数の公倍数を求めましたが、整数が3つでも5つでも、解答作業は面倒になりますが、それぞれの整数の倍数を書きだして、その後に共通の倍数を探すという手順は同じです。公倍数の求め方は理解できたでしょうか。
