ベクトルの意味と計算方法
学習する学年:高校生
1.ベクトルとスカラーの違い
高校生になると、数学の時間に矢印の形をした記号(有向線分)を扱うベクトルの勉強が始まります。
ベクトルは中学生の時に学んできた1次方程式や2次方程式などとは何か違うものだと感じて、矢印を足したり引いたりして計算できるので取っ付き難いと思った方がいるのではないでしょうか。
ベクトルは一体何を表そうとしていると思いますか?
ベクトルは、幾何学的な空間において、大きさ(量)と方向(向き)の2つの要素を表しています。
つまり、座標に有向線分を書いて、
- 大きさ
- 方向
を表すことができるということです。
ベクトルとは、1次方程式や2次方程式などの計算とは全くの別物なんです。
みなさんは、ベクトルの他にスカラーという呼び方を聞いたことはありますか?
スカラーとは、大きさ(量)だけを表していることなので方向は関係ありません。
中学生までは、主にスカラーという大きさだけを扱ってきたと思いますが、高校生からはベクトルを使うことによって大きさに加えて方向も表現できるようになります。
ベクトルは、次のような矢印で描かれます。
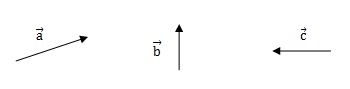
矢印のことを有向線分といい、矢印の長さが大きさ(量)を表し、矢印の向きが方向を表しています。
矢印側の端を終点、矢印の反対側の端を始点をいいます。
それぞぞれの記号の呼び方は、
- aの上に矢印が書かれたものはベクトルa
- bの上に矢印が書かれたものはベクトルb
- cの上に矢印が書かれたものはベクトルc
と呼びます。
ベクトルの意味が理解できたところで、次はベクトルの計算方法を説明していきます。
2.ベクトルの足し算と引き算の計算
ベクトルとは、大きさと方向を持っていることでしたね。
この、大きさと方向はいくつでも組み合わせて足したり引いたりして計算することができます。
ベクトルの足し算は足していくだけなので難しくないですが、ベクトルの引き算をするには少しコツがいります。
ベクトルの引き算が苦手という方は、ベクトルを眺めていても理解できないので、ベクトルを移動させてみてコツをつかむことが理解する近道です。
それでは、ベクトルの足し算と引き算の求め方について見ていきましょう。
ベクトルの足し算1
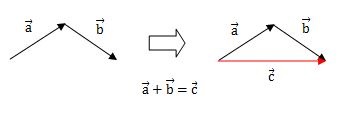
足し算1のベクトルは普通に足してもらうと答えはでます。
ベクトルの足し方ですが、ベクトルaの終点に平行移動させたベクトルbの始点を重ね合わせるだけです。
※上の図ではすでに重ね合わされている状態なので何もしなくて大丈夫です。
後は、ベクトルaの始点(矢印のつけ根)からベクトルbの終点(矢印の先端)に向けてベクトルc(赤い矢印)を描いてください。
ベクトルc(赤い矢印)がベクトルaとbを足し合わせた計算結果です。
この場合は、ベクトルの始めとベクトルの終わりを結ぶだけなので簡単でしたね。
ベクトルの足し算2
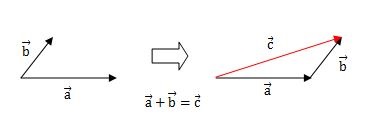
足し算2のベクトルは、ベクトルbを動かしてもらうと答えはでます。
ベクトルの足し方ですが、ベクトルbを平行移動して、ベクトルaの終点(矢印の先端)にくっつけた後にベクトルc(赤い矢印)を描いてください。
ベクトルc(赤い矢印)がベクトルaとbを足し合わせた計算結果です。
この場合は、ベクトルbを移動させ、後は普通にベクトルの始めとベクトルの終わりを結んで答えをだします。
なお、ベクトルの足し算は物理の授業で勉強する力の合成を活用しても求めることができます。
ベクトルの引き算1
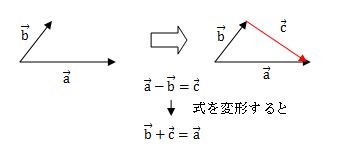
引き算1のベクトルは、ちょっとややこしいので、式を変形してみるとわかり易いかも知れません。
式を変形すると、ベクトルb+ベクトルc=ベクトルaになります。
したがって、ベクトルc(赤い矢印)が計算結果です。
この場合は式を変形しましたが、下のベクトルの引き算2のようにオーソドックスにベクトルbを逆ベクトルにして移動させる方法でも答えはでます。
ベクトルの引き算2
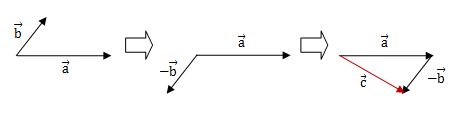
引き算2のベクトルは引き算1を違う方法で計算してみました。
もう1つの引き算の方法は、ベクトルbを逆向きにして、マイナスベクトルb(逆ベクトル)にして足していきます。
したがって、ベクトルc(赤い矢印)が計算結果です。ベクトルbをマイナスベクトルbにして、ベクトルaの終点に平行移動させれば、後は普通にベクトルの始めとベクトルの終わりを結んでもらうと答えはでます。
ベクトルの引き算1でもベクトルの引き算2でも、計算結果のベクトルcは同じ大きさで同じ向きになりました。わかりやすい方で覚えましょう。
※ベクトルの始点と終点の場所はどこでもよく、大きさと向きが同じならベクトルは等しいと解釈されます。
現在高校生で理系の大学に進学される方は、毎日のようにベクトルと向き合わなければいけませんのでしっかり内容を理解しましょう。
