比例、反比例
学習する学年:小学生
1.比例の説明
みなさんは、小学生の時の算数の時間に数が比例して増加する、比例して大きくなるなどという勉強をしたと思いますが覚えていますか?
この比例という言葉を文全体から推測するとぼんやりとわかったように感じてしまいますが正しく説明できますでしょうか。
比例とは、2つの変数xとyがあるとき、次の式で表される関係のことです。
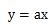
上記の式の場合は、yはxに比例するといいます。
aは比例定数といい、yがどのくらいの割合で増えていくのかを表しています。
比例のイメージをつかむためにグラフを描いてみましょう。
比例定数a=1の時のy=xの比例関係を下のグラフに描きました。
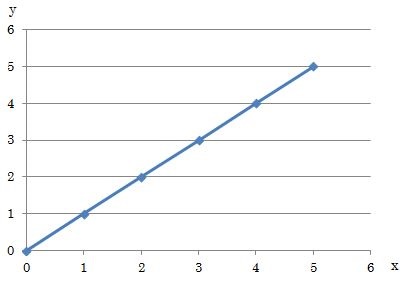
グラフを見ると、比例する場合は数が原点を通り一直線で変化していき、xの値が2倍、3倍になるとyの値も2倍、3倍になっていることがわかります。
つまり、ただ増えているのではなく、一方が増えれば、もう一方も同じ割合で増えている現象が比例です。
次は、比例定数a=2の時のy=xの比例関係を考えてみましょう。xの値が0倍の時yの値は0、xの値が1倍の時yの値は2、xの値が2倍の時yの値は4、xの値が3倍の時yの値は6、xの値が4倍の時yの値は8となります。
グラフを見て比例かどうかの見分け方ですが、y÷xをしてどこでも比例定数が同じ値になった場合は比例しています。
このように、xの値の変化量とyの値の変化量が常に一定の比例定数aで推移する関係のことを比例といいます。
2.反比例の説明
反比例は比例に反がついているので比例の逆数のことです。
詳しく説明すると、反比例とは、2つの変数xとyがあるとき、次の式で表される関係のことです。
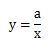
上記の式の場合は、yはxに反比例するといいます。
aは比例定数といい、yがどのくらいの割合で減っていくのかを表しています。
反比例のイメージをつかむためにグラフを描いてみましょう。
比例定数a=5の時の反比例の関係を、下のグラフに描きました。
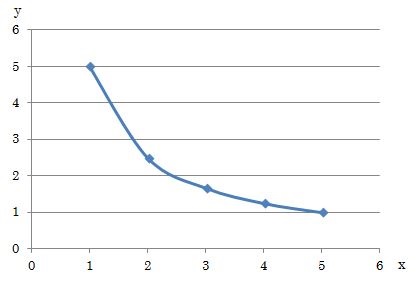
比例する場合は数が原点を通り一直線に変化していくのに対して、反比例する場合は原点を通らずに双曲線になり、xの値が2倍、3倍になるとyの値は1/2倍、1/3倍になっていることがわかります。
反比例のグラフはわかりにくいですが、xの値の変化量とyの値の変化量を掛け合わせた時に常に一定の比例定数aで推移する関係のことを反比例といいます。
上のグラフから計算すると、
- x=1の時y=5なので、1×5=5
- x=2の時y=2.5なので、2×2.5=5
- x=5の時y=1なので、5×1=5
となります。つまり、どこでも5なので反比例となります。
比例、反比例という言葉は数学の授業では頻繁に出てきますし、高校生の物理の授業や理工学系の大学の学部に進学される方も毎日のように目にすると思います。
比例・反比例という言葉は、何かを結論付けたり証明したりするときによく使いますので意味をしっかり覚えましょう。
