無理数
学習する学年:中学生
1.無理数の説明
無理数は、いまいちよく理解できないと悩んでいる方がおられると思いますが、まずは実数について思い出してください。
実数は有理数と無理数に分かれていますよね。有理数と無理数はどういう数か覚えていますか?
- 有理数:分数で表すことができる数
- 無理数:分数で表すことができない数
簡単に説明すると、分数で表すことができる有理数と分数で表すことができない無理数を1つにまとめたものが実数です。
そして、直線上で数を表す数直線はこの有理数と無理数を合わせた実数の数で満たされることになります。
したがって、分数で表すことができる数と分数で表すことができない数で実数の数直線を表さなければいけないので、無理数は実数の中の有理数ではない数のことを表しています。
わかりやすくいうと、分数の分母と分子の数が整数で表すことができない数が無理数です。
実数は有理数と無理数で表していることを覚えておいてください。
2.無理数の数の例
無理数とは、分数で表すことができない数のことです。
例えば、次のような円周率πやルートの数は、整数を使った分数で表すことができないので無理数であることがわかります。
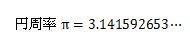
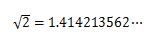
無理数と間違えやすい数としては、
- 0.09090909・・・のように同じ数字が循環する数
- 0.33333333・・・のように同じ数字が永遠と続く数
は無理数と思われるかもしれません。
しかしこれらの数は、
- 0.0909・・・=1/11
- 0.3333・・・=1/3
となり、整数を使った分数で表されますので有理数となります。
このように、整数÷整数、整数/整数のような分数の形で表すことができる数を有理数、そうでない数を無理数といいます。
無理数と有理数を間違えないようにしましょう。
