円周率π
学習する学年:小学生
1.円周率の説明
小学生の時に、算数の図形の授業で先生が黒板に丸い円を描いてこの円の円周率π(パイ)はどうのこうの・・・、と言って教えられたと思います。
円・円周率のこと覚えていますか?
まず、円とは下のような図形のことで、円の中心と円周(円の外側の線)で構成させています。
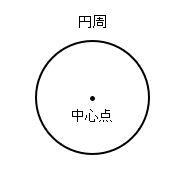
円周という言葉が出てきましたが、円周とは円の外側の長さのことですよね。
では、円周率とは何かというと、円周と直径との比率のことを表しています。率という言葉の意味は比率ということを頭に入れてください。
もっと簡単に言うと、円周の長さは直径の長さの何倍なのかということを表しています。
円周率を式で表すと次のようになります。
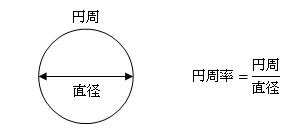
この円周率の式は学校で嫌なくらい教えられたと思いますが、なんとなく思い出してきましたか?
上の式を見ると、円周率は円周割る直径(円周÷直径)で求められることがわかります。
つまり、円周率とは円周と直径との比率のことなんです。
2.正六角形の外周と直径との比率の計算
円周率の意味を理解するために、ここでは正六角形を例にして外周と直径の比率を計算してみましょう。
正六角形は、正三角形が6コくっついてできています。
この正三角形の辺を1とすると、正六角形の外周を全部足すと6、直径は2になります。
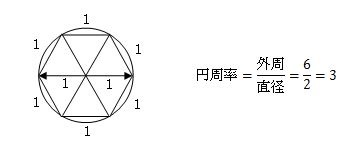
円周率の式を使って、この外周と直径を元に計算すると、正六角形の外周と直径との比率は3になります。
この状態ではまだ円になっていませんので、円周率(円周と直径との比率)は、3より少し大きいかなと直感でわかると思います。
はるか昔、円周率は3であると教えようとしていた人たちがいましたが、3とは円周率ではなく正六角形の比率だったんですね。
したがって、円周率は3.14ですが3.14じゃ計算が面倒くさいから3で計算してしまうと正しい円ではなくなってしまうので気をつけてください。
3.正しい円周率はいくつ?
正しい円周率πの値は3. 14159265358979・・・です。
数字は永遠に続きますので、π=3.14と短くして使ってください。
今回は、正六角形だけ比率を計算しましたが多角形にしていくと3.14に近づいていきます。興味が湧いた方は計算してみてください。
では最後に、下にある図と式は小学校で教えられる円周を求める公式です。
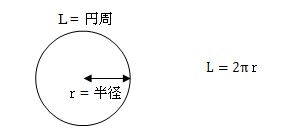
L=円周、r=半径とすると、L=2πrとなります。
円周率がわかれば円周を数値で求めることができます。
円周率πの値は、図形の面積や体積などの計算に応用できますので、ぜひ覚えてください。
