三角関数
学習する学年:高校生
1.sin, cos, tanの説明
みなさんは、sin,cos,tanという言葉を見たことはありますか?
何やら暗号のような文字に見えますが、これらの言葉は数学の三角関数を勉強していると嫌になるくらい目にします。
それぞれのsin,cos,tanの文字の呼び方は、
- sin:サイン
- cos:コサイン
- tan:タンジェント
といいます。
sinはシン、cosはコス、tanはタンではありませんので間違えないようにしてください。
sin,cos,tanは何を表しているのかというと、三角形の角の大きさと線分の長さの関係を表したものです。
簡単に説明すると、
- sinは角度に対する垂直方向の線分の長さ
- cosはは角度に対する水平方向の線分の長さ
- tanは斜辺の傾き
を表しています。
三角関数は高校生のときに学んだと思いますが…
余程のことがない限り普段の生活では使わないので忘れてしまいますね。
高校生の時に勉強したけど理解できなかった方も、三角関数についてなるべくやさしく説明していますので勉強の参考にしてください。
2.sin(サイン)の式とグラフ
下の式が三角関数のsinθの式になります。
sinθの記号はサインシータと呼びます。
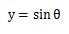
このsinθの式をθの変化(角度の変化)に応じてグラフに表すと次のようになります。
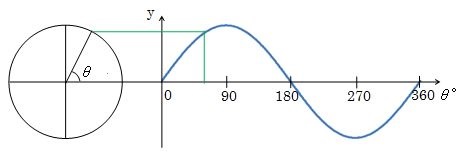
上のグラフの左側に描いてある半径が1である円(単位円)の中に、横軸を始線として一般角θ(回転角度のことです)の一本の線(動径)が引いてあります。
sinθの式の導き方は、sinθ=y/単位円の半径なので、sinθ=y/1、sinθ=yとなります。
その線(動径)と円が交りあったところから右側に直線を伸ばし、単位円の一般角θと右側のグラフのθとを対応させた箇所に点をプロットして0°~360°まで描くと波のような波形を描くことができます。
この描かれたグラフが単位円の角度θ(シータ)に対するsinの長さ(yの線分)の関係になります。
sinは角度に対する垂直方向の線分の長さを表しているので、角度θが変われば長さyが変わっていますよね。
例えば、角度が0度の時の長さyは0、角度が90度の時の長さyは1になります。
この波を見れればわかると思いますが、角度が180度を超えて360度未満の間は長さはマイナスになります。360度以降は再び0度からの動きを繰り返します。
つまり、yの値は角度の変化に応じて、+1~-1の間をいったりきたりしているということです。
sinθの波のことを、正弦曲線、正弦波、サインカーブなどといいます。
3.cos(コサイン)の式とグラフ
下の式が三角関数のcosθの式です。
cosθの記号はコサインシータと呼びます。
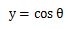
このcosθの式をθの変化(角度の変化)に応じてグラフに表すと次のようになります。
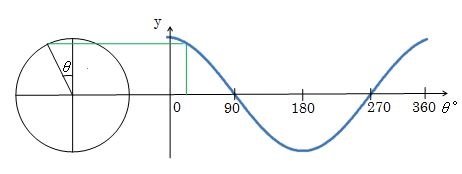
上のグラフの左側の半径1の円(単位円)の中にある一般角θは、sinの時から90度移動したところがゼロ度になって始まっていますね。
cosθの式の導き方は、cosθ=y/単位円の半径なので、cosθ=y/1、cosθ=yとなります。
cosは角度に対する水平方向の線分の長さを表しているので、角度θが変われば長さyが変わるようにθの始まる位置が90度ずらしてあります。sinとcosでは始まる位置が異なりますので間違えないようにしましょう。
動径と円が交りあったところから右側に直線を伸ばし、単位円の一般角θと右側のグラフのθとを対応させた箇所に点をプロットして0°~360°まで描くと波のような波形を描くことができます。
この描かれたグラフが単位円の角度θ(シータ)に対するcosの長さ(yの線分)になります。
例えば、角度が0度の時の長さyは1、角度が90度の時の長さyは0になります。
cosの場合は、角度が90度を超えて270度未満の間は長さはマイナスになります。360度以降は再び0度からの動きを繰り返します。
つまり、yの値は角度の変化に応じて、+1~-1の間をいったりきたりしているということです。
cosθとsinθは何が違うのかというと90度ずれていることです。cosθの波のことを、余弦曲線、余弦波、コサインカーブなどといいます。
なお、教科書などはx=cosθとなっていますが、x軸の線分の長さを表しているからです。θの始線をx軸として上の図の波を単位円の下側に90度回転させて配置した後にyをxに変えるか、上側に90度回転させて配置した後にyをxに変えて矢印の向きを右向きとなるように波のグラフ全体をひっくり返してもらうとx=cosθを表す波になります。x=でもy=でも角度に対する線分の長さは変わりはありません。x=sinθであっても同じような要領でy=sinθの波を移動させて考えてみてください。
4.tan(タンジェント)の式とグラフ
下の式が三角関数のtanθの式です。
tanθの記号はタンジェントシータと呼びます。
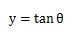
このtanθの式をθの変化(角度の変化)に応じてグラフで表すと次のようになります。
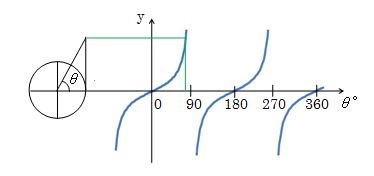
tanθのグラフは、sinθとcosθのグラフとは明らかに違いますよね。
tanθはy座標から読み取れますが、いままでと違うところは、sinθ、cosθは円(単位円)の中に三角形ができていてその三角形の頂点と円弧が交りあっていましたが、tanθの場合は円(単位円)の外に三角形ができているので頂点は円弧と交り合っていないことです。
また、90度、270度のときは値はありません(存在しません)し、値がない前後では値は+無限大・-無限大となりますので間違えないようにしましょう。
tanθの特徴は、漸近線(ぜんきんせん)で180度ごとに同じ動きを繰り返します。
5.sin,cosを三平方の定理に応用する
ここまでの説明のように、三角関数のsinθ、cosθ、tanθは角度に対する線分の長さを表していることが理解できたと思います。
みなさんは、三平方の定理を覚えていますか?
下の図をみてください。
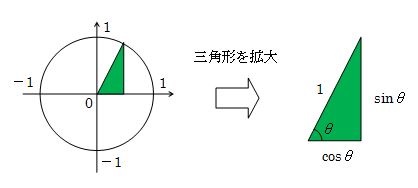
この三平方の定理をsin、cosを使って表すことができるような気がしませんか?
三平方の定理の式にsinとcosを当てはめてみると、次のような式になりました。
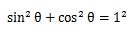
この式を変形すると
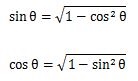
になります。
sinの値がわかればcosの値を求めることができ、cosの値がわかればsinの値が求めることができるということです。わかりましたでしょうか。
