高校数学の微分に出てくる導関数の説明

学習する学年：高校生

１．導関数の説明

前項では、微分係数 について説明しましたが、微分係数の意味はどういうものだったのか覚えていますか？

微分係数とは、関数y=f(x)のグラフのある区間の幅を狭めて限りなく0にして極限値（特定の1点の接線の傾き）について求めるものでしたよね。

ここで、導関数の仕組みを理解する為に、この微分係数という考え方をさらに拡張してみましょう。

この1点の接線の傾きについてだけを求めるのではなく、どこの点でも微分係数を求められるようにすると便利になると思いませんか？

そのような便利な方法があるんです。微分係数を a ではなく x の関数で表すようにすると、1点だけではなくどこの点でも接線の傾きを求めることができるようになります。

下の図を見てください。関数y=f(x)のグラフです。

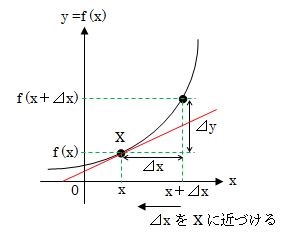
ある点を a ではなく x として表すと、 x の関数になりますね。その x の関数で表したy=f'(x)を、y=f(x)の導関数といいます。

導関数の公式は、次のようになります。

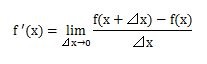
要するに、導関数は微分係数のaをxに置き換えただけの式なので、関数y=f(x)を微分して導関数y=f'(x)を求めてから、xに値aを代入すれば微分係数y=f'(a)を求めることができます。

このようにすれば、関数f(x)における様々な点の微分係数がどのようになっているのかがわかるようになります。

一般に、関数y=f(x)から導関数y=f'(x)を求めることを微分するといいます。

つまり、導関数＝微分という意味です。微分係数から発展させた関数が導関数＝微分となります。

２．微分の公式の説明

実際に微分を計算する時は上記の導関数の式を使うのではなく、次の2つの微分の公式を使って行うことが普通です。

• y=xⁿを微分するとy'=nx^n-1になる
• y=cを微分するとy'=0になる

※n=正の整数、c=定数、y'とはyを1回微分することです。

微分の公式を見てもらったところで、微分の計算を1つしてみましょう。

では、上の微分の公式を使ってy=2x³＋4を微分してみてください。

各数を微分の公式に当てはめてみると、

• y'=2×3x^3-1＋0

となるので、計算結果はy'=6x²です。

また、y'の値でyのグラフのおおよその形を判断する時は、

• y'が0より大きい区間は、yの接線の傾きは右上がりのグラフ
• y'が0より小さい区間は、yの接線の傾きは右下がりのグラフ
• y'が0の時は、yの接線の傾きは0のグラフ

となります。

微分とは、どういうことをしてるのかという内容がわかってもらえたでしょうか。

３．微分記号について

微分の勉強をしていると、数学の計算が得意な方でも普段見慣れない特殊記号がたくさん出てきて戸惑うことがありますよね。

例えば、微分をする記号といえば、f'(x)やy'をよく使いますが、dy/dxという記号も使うこともあります。

したがって、微分することを次のような記号を使っても表すこともできます。

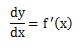
上の記号は、どのように読むかというと、ディーワイディーエックスと読みます。

dy、dxのそれぞれのd（ディー）は、⊿（デルタと読み微小な変量）よりもさらに微小な量という意味です。本当にすごく小さいという意味を表現しています。

微分は微小量を取り扱って計算しているというイメージを持ってもらうと受け入れやすくなります。