数学の微分係数の説明

学習する学年：高校生

１．微分係数について

前項では、平均変化率 について説明しました。

みなさんは、平均変化率とはどのような意味のことだったか覚えていますか？

下のグラフを見てください。

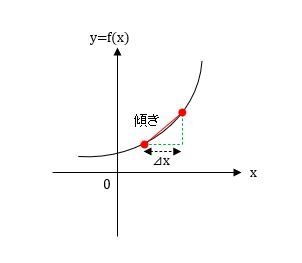
平均変化率とは、関数y=f(x)のグラフの⊿xというある特定の幅の間の線分の平均的な傾きのことでしたね。

なんとなく平均変化率のことを思い出しましたか。

ここで、みなさんに質問をします。少し考えてみてください。この⊿xをどんどん小さくしていき限りなくゼロに近づけていくとどうなるでしょうか？

特定の幅ではなく、ある1点での接線の傾きになると思いませんか。そのある1点での接線の傾きのことを微分係数といいます。

２．微分の方法

微分の公式は覚えたんだけど、実際に微分って一体何をやっているのかさっぱりわからないという方は、以下の説明をしっかり読んでみてください。なんとなく微分ってどういうことなのかが理解できると思います。

まず、下の図を見てください。

ある関数y=f(x)の式をグラフに表したものです。このグラフのX軸のA点とB点の間の⊿xをA点に限りなく近づけていった時を考えてみましょう。

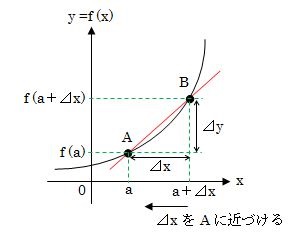
a点に向かって⊿xの幅を小さくしていくとB点がA点の方に徐々に移動していきますよね。そして、B点がA点に重なる（限りなく重なりそうになる）と、平均的な傾きが、ある1点での傾きに変わると思いませんか？

その時の1点が接点でその傾きが接線の傾きといいます。この1点における接線の傾きを求めることが微分をしているという意味合いになります。

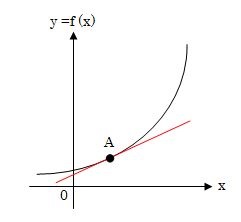
要するに、微分すると接線の傾きがわかるというとは、ある区間の平均的な変化ではなく一瞬の変化がわかるようになるということです。

もっと簡単に説明すると割り算をしているようなイメージになります。

３．微分係数を求める式

微分では、上で説明したように、平均的な傾きではなくある1点での傾きを扱わなくてはいけませんので、限りなくゼロに近づけるという考え方が重要になります。

微分係数を求める式は、平均変化率の式に限りなくゼロに近づけるという記号をつけ加えて表します。

関数y＝f(x)のx＝aのときの微分係数は、次の式になります。

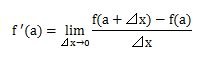
この式を解くと⊿xが限りなくゼロに近づき平均変化率が一定になる時の値が極限値といい、つまり、関数f(x)のx＝aにおける微分係数といいます。

例えば、関数f(x)=x²、x=1の時の微分係数を上の式を使って求めてみると次のようになります。

f'(1)=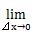f(1＋⊿x)－f(1)／⊿x

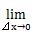＝(1＋⊿x)²－1²／⊿x

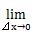＝2⊿x＋⊿x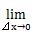²／⊿x

＝2＋⊿x

＝2＋0＝2

微分係数は2となりました。

微分の勉強をしていると、f '(x)と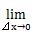の記号がよくでてきますよね。記号の意味はわかりますか？

各記号の意味を説明しますと、f '(x)のf (x)は関数という意味です。f '(x)の「'」は1回微分して導関数を求めるという意味です。もし、「''」となっていたら2階微分のことなので微分を2回しますという意味です。

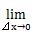はリミットと読み極限を表しています。⊿xを限りなくゼロに近づけますという意味です。⊿xはゼロになるのではありませんが限りなくゼロに近いのでゼロを代入して計算します。その時の値を極限値といいます。