平均変化率
学習する学年:高校生
1.平均変化率について
前項では、直線の傾き について説明しました。
直線の傾きとはどのようなことを表しているか覚えていますか?
傾きとは、y=f(x)の関数の式がどのくらいの割合で傾いているのかということで、xとyの変化量に関係していましたね。
今回勉強することは平均変化率です。平均変化率も、xとyの変化量に関係しています。
まずは、1次関数は直線のグラフ、2次関数は曲線のグラフになることを覚えてください。
関数y=f(x)のグラフを描いた時、1次関数は直線なのでどこの範囲をとっても傾きは同じでしたが、2次関数は曲線(放物線)なので場所によって傾きが変わってしまいます。
そこで、線分の傾きが変わってしまわないように、曲線をある点からある点まで直線で平らにしてしまった平均的な傾きにします。
そのことを、平均変化率といって、次の公式で表します。
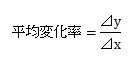
上の式に書かれている⊿yはyの変化量、⊿xはxの変化量のことです。忘れないようにしてください。
xの値がある値からある値まで変化するとyの値も変化するので、その時のxとyの変化量(⊿xと⊿y)の比にすれば変化率がわかるということです。⊿はデルタと読み、意味は微小量という意味です。きわめて小さいという意味として覚えてください。
また、平均変化率の⊿xと⊿yをもう少し詳しく説明してみると、xの値がa~bまで変化した時に、yの変化量とxの変化量を表すと次のようになります。
- yの変化量:f(b)-f(a)
- xの変化量:b-a
したがって、平均変化率の式は次のように表わすことができます。
- 平均変化率=f(b)-f(a)/b-a
例えば、関数y=3x2において、x=1から3まで変化した時の平均変化率を求めてみると、
- x=1の時のyの値:3×12=3
- x=3の時のyの値:3×32=27
となるので、上記の平均変化率の式に代入すれば、27-3/3-1を計算すれば求まります。
答えは、12です。
平均変化率を計算すればxの値の変化に対してyの値の変化を見れるので、xとyの変化量の割合を知ることができます。
2.平均変化率の計算
まず初めに、下のグラフを見てください。ある関数y=f(x)の曲線を描いたグラフです。
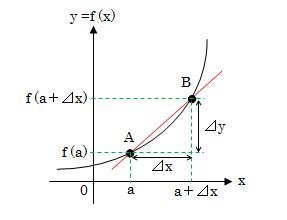
このグラフに描いてある曲線の、A点(a,f(a))からB点(a+⊿x,f(a+⊿x))までの平均変化率を求めてみましょう。
まず、平均変化率を求める⊿xと⊿yの範囲を決めます。
ここでは、
- ⊿x:a~a+⊿x
- ⊿y:f(a)~f(a+⊿x)
とします。
次の作業は、⊿xと⊿yを平均変化率の式にあてはめてみます。

となりました。
この式に数字を入れて計算していけば具体的な平均変化率の値を求めることができます。
少し複雑なことをしていて難しいと思われたかもしれませんが、平均変化率を求める時にやっていることは、範囲を指定してy/xを計算しているだけですので、何回でもグラフと式を眺めてみてコツをつかんでください。
なお、平均変化率はある1点の変化率(接線の傾き)ではなく、ある区間の変化率(線分の傾き)を求めているので混同しないようにしてください。
