関数の直線の傾きの求め方

学習する学年：高校生

１．傾きとは

高校の数学の授業で傾きという言葉聞いたことはありますか？

傾きとは、xの変化量に対するyの変化量の比のことです。

グラフに描いた関数の直線はどのくらい傾いているのか数値で表すことができます。

高校生になると微分の授業が始まりますが、微分という言葉を聞いたことはありますか？

微分っていったい何をするものでしょう？

高校生の時に微分の公式を覚えて計算して答えをだして問題を解いたけど、微分する意味が全くわからなかった人もいると思います。

微分とは早い話が接線の傾きを求めているんです。接線の傾きとは何かというとグラフを描けばイメージはつかめます。

まずは、微分の説明に入る前に関数の簡単な傾きについて見てみましょう。

２．傾きの計算１

下のグラフを見てください。

関数y=2xの直線の傾きはいくつになるでしょう？

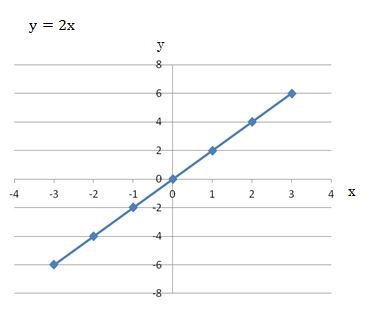
1次式が理解されている方は、傾きは2であるとすぐにわかると思いますが、微分を少しでも理解できるようにする為に傾きの求め方について説明します。

傾きとは、右に1移動したときの高さのことを言っています。

傾きを求めるには次の公式を使います。

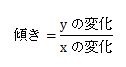
変化とはある範囲の値のことです。

xが0～1の範囲なら、x,yの変化はグラフから読み取ると、

• x＝1－0＝1
• y＝2－0＝2

となります。

xが1～3の範囲なら、x,yの変化はグラフから読み取ると、

• x＝3－1＝2
• y＝6－2＝4

となります。

どの範囲を使っても構いません。

それぞれの変化を公式に代入すると、

となります。

右に1移動したときの高さは2なので、このグラフの傾きは2となりました。

直線の場合は、どの範囲を使っても傾きは同じになります。

３．傾きの計算２

それでは、次のy=2のグラフの傾きはいくつになるでしょうか？

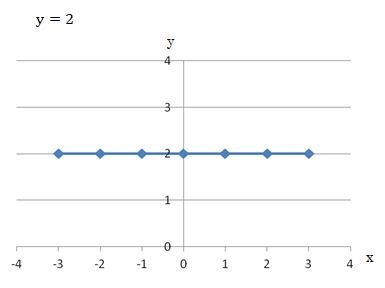
う～ん、見る限り直線は傾いているようには見えないですね。

一応、傾きを求める公式に入れて計算してみましょう。

xが0～1の範囲を使ってみます。

xとyの変化は、

• x＝1－0＝1
• y＝2－2＝0

なので、傾きの式に代入すると、

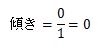
となります。

右に1移動したときの高さはまったく変わっていませんので傾きはゼロです。

やっぱり傾いていませんでした。

このように、傾きとは、関数の直線の傾き具合がどのくらい傾いているのかを表す数値のことです。

微分をわかりやすくするには傾きとは何のことを表しているのか覚えるようにしてください。