式のプラスとマイナスの符号の変換方法
学習する学年:中学生
1.式の符号の変換方法
みなさんは、中学生の時にプラス(+)とマイナス(-)の符号が混ざった数の取り扱いについて勉強したと思いますが覚えていますか?
式にプラスとマイナスの符号とカッコがゴチャゴチャしていて、きっぱり数学が嫌いになってしまった方がいますよね。
そのような方は、プラスとマイナスの符号が組み合わされた数にはプラスとマイナスの符号を変える為の4つのルールがあるので覚えてください。
そのルールに当てはめてもらえば簡単にプラスをマイナスの符号へ、マイナスをプラスの符号へ変換できるようになります。
では、符号が組み合わされた数はどのような変換ルールがあるのかというと、次のように符号を変えることができます。全部で4パターンありますので、1つずつ覚えて理解してください。
- プラス(プラスの数)=プラスの数
- プラス(マイナスの数)=マイナスの数
- マイナス(プラスの数)=マイナスの数
- マイナス(マイマスの数)=プラスの数
上記は日本語で説明していていまいち理解できないかもしれませんが、プラスのところは+、マイナスのところは-、数のところは数字を入れてもらうとわかりやすいです。
符号の変換のルールがわかったところで、次は変換のルールに数や符号を当てはめて変換してみましょう。
例えば、次のように数字の5をあてはめてみて、上記で説明したルールに従って確認してみましょう。
- +(+5)=+5
- +(-5)=-5
- -(+5)=-5
- -(-5)=+5
数を入れてプラスとマイナスの符号の変換を確認すると、なにかしらの規則があるように思いませんか。
このルールをわかりやすく考えるには、プラスの符号を省略した状態を思い浮かべてください。
では、プラスの符号を取り除いて見ると
- 5
- -5
- -(5)
- -(-5)
となります。
1~3は符号変換は簡単にできましたね。
-(-5)はわかりにくいと思いますが、次のように考えるとわかりやすいと思います。
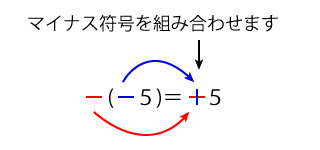
理解できましたか。マイナスの符号を十字に組み合わせると+5となります。
ルールを覚えていればプラスとマイナスの符号の変換は難しくはありませんよね。
2.式を符号変換してみましょう
プラスとマイナスの符号の変換方法がわかってもらえたと思いますので、練習の為に式の符号を変換してもらいます。
次の式を、-( )の形に変換してください。
- 5+2=
- 5-2=
- -5+2=
- -5-2=
プラスとマイナスの符号がゴチャゴチャしていますが変換のルールを使えば簡単にできます。
変換した答えは次の通りです。
- 5+2=-(-5-2)
- 5-2=-(-5+2)
- -5+2=-(+5-2)
- -5-2=-(+5+2)
符号の変換をしていないものと、変換したものを見比べてください。計算しやすくなったものがありませんか。
これは計算をする上での基本となるルールです。
人それぞれ計算しやすい方法があると思いますので、符号の変換を有効に使って計算をどのようにしたら簡単にできるのか考えてみてください。
