数学の不定積分の説明

学習する学年：高校生

１．不定積分の説明

積分には、不定積分と定積分の2つあることをご存じでしょうか。

不定積分とは、積分の範囲をどこからどこまで、という範囲を指定していませんので、積分の範囲が不定になっている積分のことです。

不定積分に対して、積分の範囲を指定している積分のことを定積分といいます。

例えば、積分の範囲を、aから始まりxで終わるとすると、このxは決まった値（定数）ではなく変数になります。積分の範囲が不定になっているということです。

また、関数y=f(x)の原始関数は定数部分を含めるといくつもあり、その中の1つの関数をy=F(x)とすると、F(x)＋Cという式にすることができます。この式を不定積分といいます。
※記号のCは積分定数なのでその中身はいくつの数でも構いません。Cを置くことにより原始関数の全ての数が1つの関数として表わされます。

不定積分は見覚えがある式ですよね。不定積分とは原始関数のことなんです。

一般的に、関数f(x)の不定積分（原始関数）を求めることをf(x)を積分するといいます。

２．不定積分をグラフに表してみましょう

初めに、下の図を見てください。ある関数y=f(x)の直線をグラフに表してみました。

下の図を使って不定積分の意味を説明していきます。

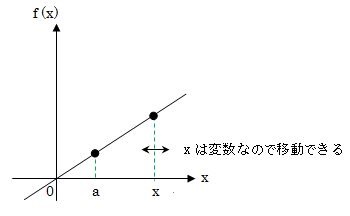
グラフのxは変数なので、積分する範囲を大きくしたり小さくしたり好きなようにできますよね。

不定積分は、定積分のようにa～bまでというような決まった範囲を積分するわけではないので、次の式で表します。

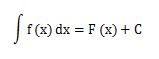
※Cは積分定数、dxは変数xについて積分するという意味です。Sが長細くなった記号は、インテグラルと呼ばれ積分をするときに使います。

では、実際に関数f(x)を積分する時はどのように計算すればいいのかというと、次のxⁿの不定積分の公式を使えば計算できます。

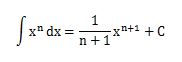
例えば、関数f(x)=x＋2を不定積分の公式に当てはめてxについて積分してみると、

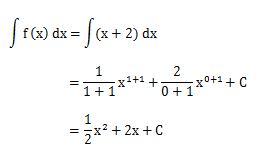
となります。

xは簡単に積分できますよね。2の積分に苦戦している方はいますか。2の積分の方法は、x⁰=1なので、2は2x⁰にして不定積分の公式に当てはめると積分できます。

なお、不定積分を求める時は積分定数Cを忘れずに付け加えてださい。

不定積分とは何をしているのかというと、関数f(x)を原始関数F(x)＋Cにしていることがわかっていただけたでしょうか。

積分の理屈が理解できてくると積分は何をしているのかイメージできるようになってきます。