定積分
学習する学年:高校生
1.定積分の説明
定積分の説明に入る前に、不定積分について説明します。
不定積分はどういう積分だったか覚えていますか?
不定積分は、積分範囲がどこからどこまでということが不変で定まっていないものでしたよね。
しかし、定積分はどこからどこまでという範囲を固定しています。
- 不定積分:範囲が定まっていない
- 定積分:範囲が定まっている
したがって、積分する積分区間がしっかり定まっているので積分の結果は数値ででてくることになります。
例えば、積分の範囲をaから始まりbで終わるとすると、このbは変数ではありませんので、ある決まった値(定数)になります。
定積分はいったい何をする為にa~bの範囲を指定して計算をしているのかというと、簡単にいうと面積を求める為です。
つまり、定積分を求めると図形の面積を計算することができるのです。
次は図形を使って定積分の意味を確かめていきましょう。
2.定積分を図を使って説明
ここで、関数y=f(x)の直線が描かれた下の図を使って定積分の意味を説明していきます。
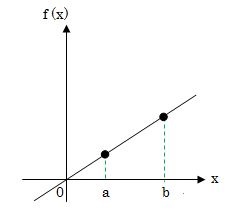
積分の範囲をある決められた範囲にすると、この図のx軸のaとbはある数値で与えられるようになります。
それでは、積分範囲aとbを決めた上の図を、a~bの間の面積を求める式にしてみましょう。
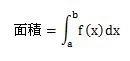
Sが長細くなった記号はインテグラルといいます。∫の下の文字(a)は下端(かたん)といいどこから積分を開始するかの値を、∫の上の文字(b)は上端(じょうたん)といいどこまで積分を続けるかの終点の値を記入します。
上記の式は不定積分の式に、a、bを付け加えただけです。
このa~bまでの定積分を求める区間を積分区間といいます。
この式を計算する時は、
- ∫baf(x)dx=[F(x)]ba=F(b)-F(a)
として計算していきます。
例えば、関数y=f(x)=2xの2~5までの積分区間の定積分を求めてみましょう。
上の定積分の式に、f(x)=2x、a=2、b=5を代入してみると次のようになります。
- ∫52(2x)dx
後は、2xを不定積分(積分)します。積分後にa,bを代入してF(b)-F(a)を計算すると答えはでます。
- ∫52(2x)dx=[x2]52=25-4=21
答えは21となりました。
定積分は変数を扱っていませんので、ある値(定数)を求めることができます。
定積分には、不定積分ででてきた積分定数C(せきぶんていすうシー)もでてきませんので馴染みやすいと思います。
定積分とはどういうものなのかなんとなく理解できたでしょうか。
