式の基本
学習する学年:中学生
1.小学校で勉強したいろいろな式の説明
小学校で勉強した算数の授業の内容は好きになれましたか。
小学校1年生から算数の勉強を本格的に始め、学年が進むにつれいろいろな式が出てくるようになります。
小学生低学年では、
- 5+3=
- 7-2=
- 4×9=
- 30÷5=
のように数のみを単純に計算して答えを求めました。
数と数との間にある記号(+、-、×、÷、=)は演算記号といい次のようになります。
- +:+の左右の値を足す為の演算記号
- -:-の左右の値を引く為の演算記号
- ×:×の左右の値を掛ける為の演算記号
- ÷:÷の左右の値を割る為の演算記号
- =:=の左辺と右辺の値が等しい意味の記号(等号という)
上記の演算記号のルールに従って、足したり、引いたり、掛けたり、割ったりできるようになり、四則演算の基本を勉強してきましたよね。
そして、学年が進んで高学年になると、カッコが付いた式が出てきます。
- (5+3)×4=
- (7-2)÷5=
このように、カッコがついていたらカッコの中から最初に計算していくルールがありましたよね。
さらに、学年が進んで中学生になると、数にアルファベット(x、y、zなど)がくっ付いている形の式がたくさん出てくるようになります。
算数・数学は数だけを扱っているのではなく、数だけでも計算できるし、数にアルファベットが付いたものも計算できるという特徴があります。
2.数にアルファベットが付いた式の説明
それでは、数にアルファベットがくっ付いた形の式の基本的な知識を勉強して理解度を深めていきましょう。
まずは、下の式をみてください。
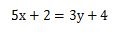
この式を1つ1つ詳しく説明していきます。
まずは、左辺、右辺、等式という言葉は式の基本となります。
- 左辺:=(イコール)の左側のこと
- 右辺:=(イコール)の右側のこと
- 等式:=(イコール)で左辺と右辺をつないだ式のこと
等式とは左辺と右辺が等しいことの意味です。
イコールでつないだ式に方程式という言葉がありますが、方程式とは式に未知数(変数)を含みその未知数が特定の値をとるもの、すなわち式=0と表せるものです。
次は、数字とアルファベットの意味を覚えましょう。
5x、2、3y、4といった、数字や数字とアルファベットがくっ付いたものを項といいます。
もし、5x、2、3y、4の前が-符号だったら-も項に含みます。
もう少し詳しくいうと、5xはx項、3yはy項、2と3は定数項です。
そして、x、yなどのアルファベットを未知数といいます。未知数とは、まだ値がわからない数のことです。
上の式では、5xのx、3yのyは未知数です。
では、5xの5、3yの3は何かというと係数です。
※係数に-符号が付いていたら-も係数に含みます。
未知数に対して既知数(きちすう)という数もあります。既知数とはすでに値がわかっている数のことです。上の式では、5、2、3、4のことです。
※5xの5、3yの3は係数でもあるし既知数でもあります。
このように、それぞれの決まった呼び方がありますので覚えましょう。
また、右辺や左辺の項を=(イコール)の向こう側に動かすことができます。
この作業のことを移項といいます。
例えば、上記の式の左辺の2を右辺へ移項してみると、下の式のように右辺には正の符号が負の符号に変化した-2が入ります。
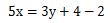
未知数が含まれている式では、最終的には移項を何回も使ってxやyの未知の値を求めていくことになります。
3.アルファベット(未知数)を使った時のルール
アルファベット(未知数)を使った式にはルールがあります。
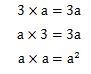
上記の3つの式を見てください。
3つの式にいえることは、数字と未知数の掛け算をする時は掛け算の演算記号が省略できます。
- 3×a→3a
そして、数字が前で記号を後ろに置いて使います。
- a×3→3a
一番下の式では、同じ記号が複数あるかけざんの時には指数を使うようになります。
- a×a→a2
このように、未知数の計算にはルールがありますので覚えてください。
4.数学のおすすめの本
お子さんが中学校に進学したので数学の勉強を頑張ってもらいたいと考えている親御さんはいませんか。中学1年生の数学の勉強がはかどるおすすめの本を紹介します。
本の名前:中1数学をひとつひとつわかりやすく
数学が得意になるには問題がすらすら解けれるようになることです。
数学が苦手とか嫌いとかいう方が数学を好きになるにはどうしたらいいのかというと、計算の基本を覚えなくてはいけません。
中学1年生で勉強する内容は、中学2年、3年生まで影響する重要な基本のことですので疎かにできません。
基本となる問題がすらすら解けれるようになると数学の学力は一気に向上しますよ。

