2次方程式の成り立ち
学習する学年:中学生
1.2次方程式の説明
中学生になると1次方程式の他に2次方程式を勉強します。
方程式の種類には、1次方程式、2次方程式、3次方程式・・・などいくつかの種類があります。
今回は、2次方程式の言葉の意味について説明します。
2次方程式の2次という意味は、未知数の一番大きい次数(何乗かということ)が2になっていることです。
例えば、式の中に、xとなっている項があれば1次、x2となっている項があれば2次ということになります。
また、式に使われている未知数の数によって、未知数が1つあれば1元、未知数が2つあれば2元、未知数が3つあれば3元などという種類があります。
- 未知数がxで1つの時=1元
- 未知数がx、yで2つの時=2元
- 未知数がx、y、zで3つの時=3元
方程式の意味は、1次方程式のときでも説明しましたが未知数を含んでいる式ということです。
方程式は、未知数(変数)であるxやyの値を求めることが目的で、方程式を満たす未知数の値を解といい、すべての解を求めることを解くといいます。
つまり、式=0の時のxやyの未知数の値を求めますので、式=0が成り立つ場合の式を方程式といい、2次方程式を解くという意味は、方程式を満たす未知数x、yのすべての値を求めることです。
2.2次方程式の構造
いままでの次数と方程式の説明をまとめると、2次方程式は次のような(1)~(3)の式のことをいいます。
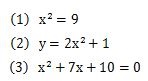
それぞれの式の説明をします。
- (1)の式の説明
- 未知数はxが1つあるので1元、xは2乗なので2次。
- よって、1元2次方程式といいます。解は式=0の時のxの値を求めます。
- (2)の式の説明
- 未知数はxとyで2つあるので2元、xは2乗、yは1乗で一番大きい乗数は2乗なので2次。
- よって、2元2次方程式といいます。解は式=0の時のxとyの値を求めます。
- (3)の式の説明
- 未知数はxが1つあるので1元、xは1乗と2乗で一番大きい乗数は2乗なので2次。
- よって、1元2次方程式といいます。解は式=0の時のxの値を求めます。
この様に、2次方程式にはいろいろな種類のものがあることが理解できたと思います。
なお、2次方程式を解く方法は、基本的には因数分解を使うか、解の公式を使うかの2種類があります。どちらを使っても構いませんので解きやすい方を使ってください。
2次方程式は1次方程式より複雑になりますが、何回でも解く練習をして計算するコツをつかみましょう。
