2次方程式の解き方（解の公式）｜もう一度やり直しの算数・数学

2次方程式の解き方（解の公式）

学習する学年：中学生

2次方程式を解くとは、2次式＝0を満たすxの値を全て求めることです。

2次方程式を解く方法には2種類あり、1つ目は因数分解を使う方法、2つ目は解の公式を使う方法でしたよね。

ここでは、2つ目の方法の2次方程式の解き方である、解の公式について説明していきます。

解の公式とは、2次方程式のax²＋bx＋c＝0を因数分解を使わずに、公式に各項の係数のa、b、cの値を代入して機械的に解いてxの値を求めてしまおうという便利な公式です。

次のように、a、b、cの値を代入してxの答えを求めてください。

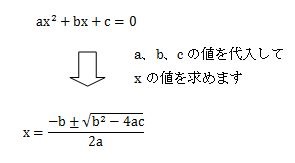
2次方程式の場合は解の公式を使えば、2次式＝0を満たすxの値を全て求めることができます。

因数分解を使って解くのか、解の公式を使って解くのかはどちらでも構いません。解きやすい方で解いてください。

但し、学校のテストの問題に因数分解で解きなさいとか、解の公式で解きなさいとか書いてあったら指示に従って解いてください。

下の2次方程式を解の公式を使って解いてみましょう。
（因数分解を使って解いた時と同じ式です。）

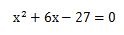
解の公式を使って解く手順は、次の順番になります。

たったこれだけの作業で答えが求まってしまいます。

気を付けてもらいたいことは、間違えずに2次方程式のa、b、cの値を解の公式に代入することです。間違えて代入すると正しい答えがでてきませんので注意してください。

それでは、解の公式を使った手順の通りに進んで2次方程式を解いていきましょう。

まず、式から、a、b、cの値を探して見ましょう。

この式のa、b、cの値は、次のようになります。

式からa、b、cの値を見つけることができましたので、計算する準備が整いました。

それでは、解の公式にa、b、cの値を代入して、解の公式を計算していきましょう。

計算の途中式は次のようになります。

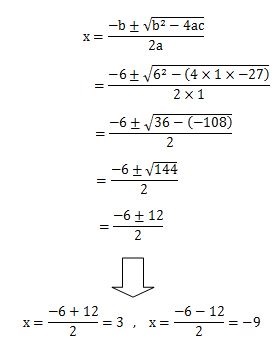
解の公式を計算すると、答えは、x=3と－9になりました。

計算結果は、因数分解を使って解を求めた時と同じ答えになりました。

因数分解と解の公式は、どちらの方法が解きやすかったですか？

因数分解でも解の公式でもどちらの方法を使っても解は同じになることがわかったでしょうか。

解の公式の中のb²－4acの部分は、2次方程式が満たされる解の判別式としても活用できます。

どういうことかというと、判別式として使うb²－4acの値が0か0より大きいか小さいかで、解が2つか1つか、実数解か虚数解かがわかります。

解の公式は、ルートの計算があったり、分数の計算もしないといけないので面倒だと思いますが、複雑な2次方程式を解く場合は断然解の公式の方が簡単に解くことができます。

また、どのような2次方程式でも何も考えずに公式の中の必要な値を代入して計算すればいいだけですので考える時間の節約にもなります。

2次方程式を解く時は解の公式を活用してみてください。