算数の割合（歩合・百分率）の計算方法

学習する学年：小学生

１．割合の説明

割合とは、全体の数や量に対する部分の数や量の関係のことです。

割合を式で表すと、次のように、部分÷全体として計算します。

割合を表す時は、主に、歩合（ぶあい）と百分率（ひゃくぶんりつ）が使われます。

歩合とは、全体を10割、又はある基準を10割として、部分の数量や基準と比べた時の数量を割（わり）、分（ぶ）、厘（りん）を使って表した割合のことです。

割は分数で10分の1（小数で0.1）、分は100分の1（0.01）、厘は1000分の1（0.001）の位を表しています。

例えば、年末や正月明けのバーゲンセールの時に、3割引、5割引などという値札が商品に貼られています。それは、商品の全体の値段に対する割合を表しています。

3割は30%、5割は50%のことです。

また、テレビで野球の中継を観ていると2割9分3厘というように打者の打率を表す時にも使われていることがわかります。

2割9分3厘は29.3%のことです。

百分率とは、全体を100％、又はある基準を100%として、部分の数量や基準と比べた時の数量がどのくらいの割合なのかを表す方法のことです。

私たちは、次のように普段の生活の中で割やパーセントという言葉をよく使いますよね。

1. 私は、算数の参考書を2割引で買いました。
   ※全体から2割り引いてくれたということなので、残りの8割の代金を支払って買ったということです。
2. 私は、この算数の参考書を30％読み終えました。
   ※全体の70%は読み終えていないということです。
3. 私は、参考書を読んで分数の計算方法を50％理解しました。
   ※全体の半分（50％）理解したということです。
4. 彼は計算が苦手だったので数学は100％理解できなかった。
   ※全く（100％）理解できなかったということです。

このように、割のことは歩合、パーセントのことは百分率のことなんです。

そのような意味合いとして、割（歩合）やパーセント（百分率）を使うことができます。

では、歩合（割・分・厘）と百分率（％）の間にはどのような関係があるのかというと、

• 12割＝120％
• 10割＝100％
• 5割＝50％
• 1割＝10％
• 3割5分2厘＝35.2％

のように表わされます。

また、歩合や百分率の他には、小数や分数で割合を表すこともあります。

割合の関係の表

歩合	百分率	小数	分数
12割	120％	1.2	6／5
5割	50％	0.5	1／2
1割5分	15％	0.15	3／20
1分	1％	0.01	1／100
1分2厘	1.2％	0.012	3／250

例えば、12割＝120％ですよね。小数で割合を表すと120／100＝1.2倍、分数で表すと1.2＝12／10＝6／5倍です。

5割＝50％ですよね。小数で割合を表すと50／100＝0.5倍、分数で表すと0.5＝5／10＝1／2倍です。

1割5分＝15％ですよね。小数で割合を表すと15／100＝0.15倍、分数で表すと3／20倍です。

このように、割合を表す方法は、歩合（割・分・厘）、百分率（％）、小数、分数の4パターンがあるということを覚えておきましょう。

２．割合（割、パーセント）の問題

割合で使う歩合、百分率、小数、分数がわかりましたよね。

割とパーセントに慣れるために上で説明したことを頭に入れて次の問題を解いてみましょう。

問題１．

9割とは何％のことでしょうか？

考え方：9割は全体の内のいくつに相当するのか分数で考えます。

全体の10の中に部分が9あるということは、9/10になりますよね。

百分率は100倍することで計算できますので、（9/10）×100＝90

したがって、9割とは90％のことです。

問題２．

100％とは何倍のことでしょうか？

考え方：100%は100の内のいくつに相当するのか分数で計算します。

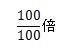
したがって、答えは、1倍になります。

問題３．

30％とは何倍のことでしょう？

考え方：30%は100の内のいくつに相当するのか分数で計算します。

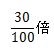
したがって、答えは、0.3倍になります。

毎日、消費税などの計算をしているので簡単ですよね。

問題４．

定価から30％引きすると8400円になる洋服があります。この洋服の定価はいくらでしょうか？

考え方：定価の7割の値段が8400円ということです。

定価×（1－0.3）=8400
定価×0.7=8400

よって

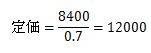
答えは、12000円になります。