三平方の定理(問題)
学習する学年:中学生
問題
次の三平方の定理の問題を解きましょう。
三平方の定理は公式があります。公式を使って辺の長さを答えましょう。
- 問1.
- 三平方の定理は別の言い方で何と言われていますか?
- 問2.
- 三平方の定理は何の関係を表すものですか?
- 問3.
- 次の三角形の辺がa、b、cであるときの三平方の定理の公式を答えましょう。
-
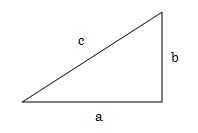
- 問4.
- 上の公式をcを求める式に変形しましょう。
- 問5.
- 上の公式をbを求める式に変形しましょう。
- 問6.
- 上の公式をaを求める式に変形しましょう。
- 問7.
- 上の図でa=3、b=2であるとき、cの値はいくらになりますか?
- 問8.
- 上の図でa=2、c=4であるとき、bの値はいくらになりますか?
- 問9.
- 上の図でb=2、c=5であるとき、aの値はいくらになりますか?
スポンサーリンク
答え
- 答1.
- 三平方の定理は、ピタゴラスの定理とも呼ばれています。
- 三平方の定理もピタゴラスの定理もどちらも同じ意味です。
- 答2.
- 三平方の定理は、直角三角形の3つの辺の長さの関係を表す公式です。
- 答3.
-
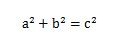
- 答4.
- c2の2乗をイコールの向こうに移行するとルートに変わります。
-
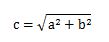
- 答5.
- b2イコールの式にすると、b2=c2-a2となります。
-
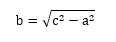
- 答6.
- a2イコールの式にすると、a2=c2-b2となります。
-
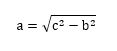
- 答7.
- 式にa=3、b=2を代入して計算してください。
-
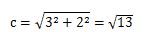
- 答8.
- c2=a2+b2をb2=に変形すると、b2=c2-a2になります。
- 式にc=4、a=2を代入して計算してください。
-
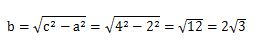
- 答9.
- c2=a2+b2をa2=に変形すると、a2=c2-b2になります。
- 式にc=5、b=2を代入して計算してください。
-
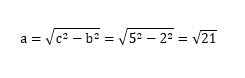
トップページへ戻る | 学年別一覧(問題)へ行く | 勉強をする
スポンサーリンク