3次関数(方程式)のグラフ
学習する学年:中学生
1.3次関数(3次方程式)の説明
今回は、3次関数(方程式)について考えてみます。
3次関数とは、未知数の一番大きい次数が3になっている関数のことをいいます。
次数とは、x3を例にすると、エックスの3乗という何乗なのかの部分のことです。この部分が3になっている式が3次関数の式となります。
つまり、次のような未知数の一番大きい乗数が3乗になっている式が3次関数といいます。
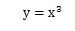
また、y=x3の他にも、y=2x3、y=5x3+1、y=10x3+x2+7、y=-2x3のような、x3が含まれている式は3次関数といいます。
3次関数の式がわかったところで、次は、3次関数をグラフに描いてみましょう。
2.3次関数(方程式)をグラフに描く
グラフとは関数を満たす点の集合のことです。
グラフを描く時は、xとyの増減表を作れば簡単にできます。
それでは、y=x3の式をグラフに描いてみましょう。
まずは、y=x3の式のxとyの値の増減表を作ってみます。
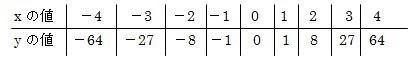
この増減表で求めたx、yの値を方眼紙にプロットして線を引けばグラフを描くことができます。
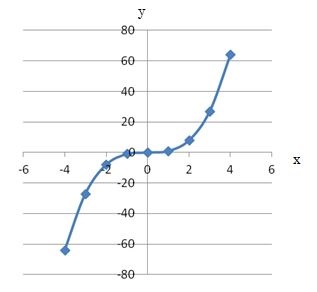
増減表から描いたグラフを見ると、xがプラスの時はyの値はプラス、xがマイナスの時はyの値はマイナスになっています。
これで、今までに勉強してきた、1次関数、2次関数、3次関数のグラフの形が把握できましたね。
次のようなグラフになります。
- 1次関数:直線
- 2次関数:放物線
- 3次関数:xがプラスの時はyの値はプラス、xがマイナスの時はyの値はマイナス
1次関数は直線、2次関数は放物線というように式からグラフの形をイメージしやすいですが、3次関数以上のグラフは、1次関数や2次関数のように単純なグラフではありません。
1次関数(方程式)のグラフや2次関数(方程式)のグラフとは全く異なった形になります。
3次関数以上はとても複雑で難しいグラフです。増減表を作ることも時間がかかりますので、こんな感じのグラフになるんだろうという概形をなんとなく覚えておいてください。
