数学の三角比（30度, 45度, 60度）についての説明

学習する学年：中学生

１．三角比って何？

三角比とは、直角三角形の3つある角の90度以外のどちらか1つの角度が決まれば、3つの辺の長さの比率が決まるという性質のことです。

注意：直角二等辺三角形の場合は角度が決まらなくても3辺の比率は決まってしまいます。

三角比として頻繁にでてくる角度は、30度と45度と60度です。

中学生では、この3つの角度の30度と45度と60度の時の三角形の比率を全て覚えておけば、数学の三角図形の問題はなんとか乗り越えられます。

それでは、30度、45度、60度の角度になっている三角形の三角比の勉強をしていきましょう。

２．三角比（30度、45度、60度）の説明

三角比の辺の比率について、下の図を使って説明します。

2つの三角形の左端の角度を見てください。

それぞれの角度は、30度の直角三角形と45度の直角二等辺三角形です。

いろいろある角度の中でこの30度と45度の角度の時は、人が覚えやすい比率になります。

この比率は本当によくでてきますし、いろいろな図形の問題に応用できますので覚えてしまいましょう。

直角三角形の左端の角度が30度の時の比率は次のようになります。

1対2対√3（いったいにたいルートさん）

（対辺a＝1、斜辺b＝2、底辺c＝√3）

直角三角形の左端の角度が45度（直角二等辺三角形）の時の比率は次のようになります。

1対1対√2（いったいいったいルートに）

（底辺a＝1、対辺b＝1、斜辺c＝√2）

1対2対√3と1対1対√2を呪文のように何回でも比率を唱えていれば覚えられますので、しっかり頭の中に叩き込みましょう。

また、1対2対√3と1対1対√2の比が、対辺、斜辺、底辺のどの辺と対応しているのかも覚えてください。

直角三角形の左端の角度が60度の場合は、左端が30度の直角三角形を回転させて左端が60度になるようにしてください。

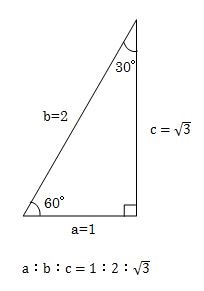
この場合は、ただ左端が30度の直角三角形を回転させただけですので、それぞれの辺の比率は変わりません。

したがって、直角三角形の左端の角度が30度のときの1対2対√3の比率を覚えておけば大丈夫です。

直角三角形の左端の角度が60度のときの比率は次のようになります。

1対2対√3（いったいにたいルートさん）

（底辺a＝1、斜辺b＝2、対辺c＝√3）

このように、30度と60度の三角比は1対2対√3、45度の三角比は1対1対√2になります。

三角比を覚えると三角形の図形の計算に悩まなくて済むようになります。三角形の角度と辺の計算問題をスムーズに行えれるようになってください。