三角比(30°,45°,60°)問題
学習する学年:中学生
問題
次の三角比の問題を解きましょう。
三角形の角度が、30°、45°、60°の時の三角比を覚えて辺の長さが計算できるようになりましょう。
- 問1.
- 三角比とはどういう性質のことですか?
- 問2.
- 三角比として頻繁にでてくる角度は何度ですか?3つ答えましょう。
- 問3.
- 次の三角形のa:b:c の比を答えましょう。
-
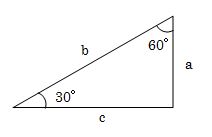
- 問4.
- 上の三角形でa=2のとき
b、c の値はいくらになりますか? - 問5.
- 上の三角形でa=√3のとき
b、c の値はいくらになりますか? - 問6.
- 次の三角形のa:b:c の比を答えましょう。
-
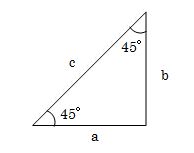
- 問7.
- 上の三角形でa=2のとき
b、c の値はいくらになりますか? - 問8.
- 次の三角形のa:b:c の比を答えましょう。
-
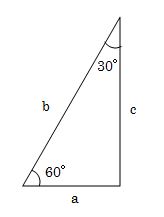
- 問9.
- 上の三角形でa=3のとき
b、c の値はいくらになりますか?
スポンサーリンク
答え
- 答1.
- 三角比は、直角三角形の3つある角の90度以外のどちらか1つの角度が決まれば、3つの辺の長さの比率が決まるという性質です。
- 答2.
- 三角比として頻繁にでてくる角度は、30度、45度、60度の3つです。
- 答3.
- 直角三角形の左端の角度が30度の時の三角比は次のようになります。
- 1対2対√3で覚えてください。
-
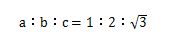
- 答4.
- 三角形の角度が30度の時の三角比を使って計算してください。
- a=2ということは、bとcは三角比を2倍すれば答えがでます。
-
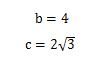
- 答5.
- 三角形の角度が30度の時の三角比を使って計算してください。
- a=√3ということは、bとcは三角比を√3倍すれば答えがでます。
-
b=2√3
c=3 - 答6.
- 直角三角形の左端の角度が45度(直角二等辺三角形)の時の三角比は次のようになります。
- 1対1対√2で覚えてください。
-
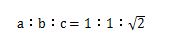
- 答7.
- 三角形の角度が45度の三角比を使って計算してください。
- a=2ということは、bとcは三角比を2倍すれば答えがでます。
-
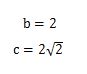
- 答8.
- 直角三角形の左端の角度が60度の時の三角比は次のようになります。
- 1対2対√3で覚えてください。
-
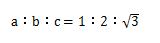
- 答9.
- 三角形の角度が60度の時の三角比を使って計算してください。
- a=3ということは、bとcは三角比を3倍すれば答えがでます。
-
b=6
c=3√3
トップページへ戻る | 学年別一覧(問題)へ行く | 勉強をする
スポンサーリンク