正弦定理
学習する学年:高校生
1.正弦定理の説明
正弦定理は、あらゆる三角形の角度とその辺の長さの関係を表した定理です。
みなさんは高校生の時に、正弦定理と余弦定理を勉強したと思いますが、余弦定理の内容は覚えていますか?
余弦定理とは、三角形のそれぞれのcos(コサイン)についての角とその角に対する辺の長さとの関係を表していました。
今回勉強する正弦定理は、三角形のそれぞれのsin(サイン)についての角とその角に対する辺の長さとの関係を表していて、どの三角形にも対応できるとても便利な公式です。
次のように、正弦定理はsinについての角を用い、余弦定理はcosについての角を用います。
- 正弦定理:sinについての角
- 余弦定理:cosについての角
正弦定理と余弦定理は似ていますが、正弦定理はsinを、余弦定理はcosを使いますので、間違えないように使ってください。
2.正弦定理の公式について
正弦定理は、次のような3つの関係式で成り立っています。
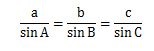
正弦定理の正弦とはsinのことを意味していますので式にsinが使われているんです。
それでは、公式をみてもらったところで、この公式を三角形の平面図形を使って説明します。
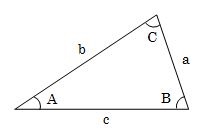
正弦定理の公式と三角形の図形を見ると、次のように三角形のある辺の長さ(a、b、c)は、それぞれの角(A、B、C)と関係していることがわかります。
角と辺の関係については、
- 角Aと辺a
- 角Bと辺b
- 角Cと辺c
はお互い向かい合っていることがわかります。
お互い向かい合っている角と辺は正弦定理の公式が成り立ちます。
この公式はどんな三角形でも成り立ちますので、いろいろな場面で使うことができます。
3.正弦定理の公式を使ってみましょう
それでは、気分転換に下の問題を解いてみましょう。
下の図の辺aの長さを求めてください。
sin35°とsin75°は、
- sin35°=0.574
- sin75°=0.966
として計算してください。
(sinは三角比の表か関数電卓で計算すると求まります。)
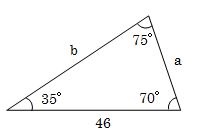
三角形の1辺の長さと2つの角度がわかれば、正弦定理を使って求めたい1辺の長さを計算することができます。
したがって、正弦定理の公式に値(sinA、sinC、辺c)を当てはめると答えが求まります。
sinA、sinC、辺cの値を書き出してみると、
- sinA:0.574
- sinC:0.966
- 辺c:46
となり、この値を公式に代入して計算を始めてください。
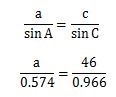
計算すると次の答えになります。
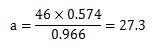
よって、答えは、a=27.3となりました。
正弦定理の公式を使えば、辺の長さと角度が計算できます。正弦定理の使い方はわかっていただけたでしょうか。
