余弦定理
学習する学年:高校生
1.余弦定理の説明
余弦定理(よげんていり)は、あらゆる三角形の角度とその辺の長さの関係を表した定理です。
みなさんは高校生の時に、余弦定理に似た言葉の正弦定理を勉強したと思いますがどんな内容だったか覚えていますか?
正弦定理とは、三角形のそれぞれのsin(サイン)についての角とその角に対する辺の長さとの関係を表していました。
今回勉強する余弦定理は、三角形のそれぞれのcos(コサイン)についての角とその角に対する辺の長さとの関係を表していて、とても便利な公式です。
このように、余弦定理はcosについての角を用いて、正弦定理はsinについての角を用います。
余弦定理と正弦定理は似ていますが、余弦定理はcosを正弦定理はsinを間違えないように使ってください。
2.余弦定理の公式について
余弦定理は、次のような3つの関係式で成り立っています。
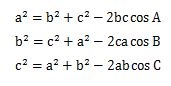
余弦定理の余弦とはcosのことを意味していますので式にcosが使われているんです。
それでは、公式をみてもらったところで、この公式を三角形の図形を使って説明します。
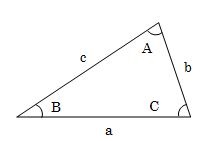
余弦定理は何を表しているのかというと、3つの辺と1つの角の関係です。
余弦定理の公式と三角形の図形を見ると、三角形のある辺の長さ(a、b、c)は、他の辺の長さとその2辺で作りだされる角と関係していることがわかります。
例えば、辺aの長さは、辺bと辺cとその2辺が作りだす角Aに関係してきます。
辺bの長さも辺cの長さもそれぞれの辺とその2辺が作りだす角に関係しています。
つまり、三角形の2辺の長さと1つの角の大きさがわかれば、余弦定理を使えばもう1つの辺の長さを計算することができるのです。
また、三角形の3辺の長さがわかれば、余弦定理を使えばすべての角の大きさも計算できます。
ここで問題です。
上の三角形の図形の角Cを90°にしたら余弦定理の公式はどうなるでしょうか?
角度を90°にすると、cos90°はゼロになりますので、次のようになります。
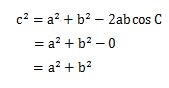
この式はどこかで見たことがありませんか?
そうなんです。勘が鋭い人はわかりますね。三平方の定理のときにでてきた式と同じだと思います。
余弦定理とは三平方の定理を拡張したものですので覚えておいてください。
