積分の考え方
学習する学年:高校生
1.積分って何?
高校に進学すると微分・積分の授業が始まります。
みなさんは、積分という言葉を聞いて何を思い浮かべますか?
難しい公式を使ってよくわからない複雑な計算をしている、というイメージを持っている方が多いのではないでしょうか。
積分は簡単にいうと、ある区間の面積を求めています。えっ、本当にそうなのと思うかもしれませんが本当に面積を求めています。
積分と同じような時期に勉強する微分は何のイメージか覚えていますか?
微分は割り算のイメージです。
ですので、微分は割り算のイメージ、積分は掛け算のイメージを持って計算してください。
積分は面積を求めているということなので、普通に面積を求める時は、
- 四角形の場合は縦×横
- 三角形の場合は底辺×高さ÷2
をして計算していますが、積分はそのような方法を使って面積を求めていません。
では、どうやって面積を求めているのか疑問に思いませんか?
ここでは、積分の基本的な意味について説明していきます。
2.積分の説明
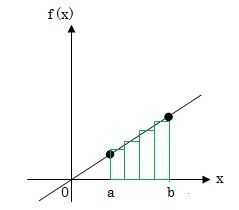
下の図を使って説明します。
例えば、下の図の横軸のa~bまでの範囲の面積を求めてみたい時を考えてみましょう。
数学の教科書に載っている積分の公式は次のようになっています。
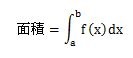
この公式は、関数f(x)を変数xの値がa~bの範囲で積分するという意味を持っています。
公式のa、bは、aは範囲の開始の位置、bは範囲の終わりの位置を表しています。
つまり、積分すると開始のa点~終わりのb点までの範囲の面積を求めているのです。
積分の面積の求め方は、まずは、関数y=f(x)の直線とa~bで囲まれた範囲を細かくいくつかの短冊形にします。
次に、この短冊形をどんどん足し合わせていきます。この作業を続けていくと最終的に面積が計算できます。
積分は、このような短冊形の方法を使って面積を求めています。
上の図はおおざっぱですのでカクカクしていますが、この短冊形の横幅を限りなく小さくする(極限にする)とカクカクは無くなると思いませんか?
微分の時にもでてきましたが、微小量dxという記号は積分でもでてきます。
積分の公式にでてくるdx(短冊形の横幅のdx)は変数xについて積分することです。とても小さいという意味を含んでいます。
ここまでの説明で、積分の式の意味は、ある区間を細かくして足し合わせて面積を求めていることが、なんとなくわかってもらえたでしょうか。
