有理化
学習する学年：中学生
１．有理化の説明
有理化（分母の有理化）とは、分数の分母の値にルート（平方根）があるときは、分母からルート（平方根）をなくしてしまいましょう、という作業を行うことです。
みなさんは、分数の構造は覚えていますか？
分数は下の説明のように分母と分子があり、分数の下の数は分母で上の数は分子です。
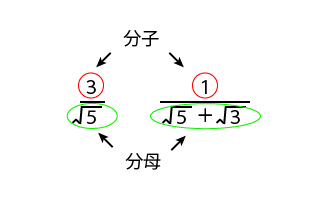
分数の分母にルートがある時は、なぜ有理化をしなければいけないのかというと、分母にルートがない方が数が見やすくなると思いませんか？
分母にルートがない数を使えば次の計算が簡単にできるようになると思いませんか？
有理化をするのは面倒だと思いますが、このように、いろいろ便利になることがありますので有理化を行わなければなりません。
２．有理化する方法
それでは、有理化する方法を説明します。
分数の分母と分子の両方の数に、分母の数を掛け合わせると有理化ができるようになります。
例えば、次のような数を有理化する場合を考えてみましょう。
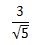
このような、分母にルートを含んだ分数を有理化するには、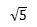
を分母と分子に掛け合わせてください。
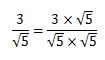
同じルートの数を2回掛け合わせれば、√5×√5＝5というように、分母のルートをなくすことができますよね。
したがって、答えは
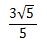
になります。
３．有理化する方法（分母にルートの足し算がある時）
もう1つ、有理化について説明します。
次のような、分数の分母にルートの足し算が含まれている式を有理化する場合を考えてみましょう。
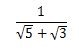
この式の分母には、ルートの数が2つありそれぞれの数を足し合わせています。
この場合は、√5だけ掛け合わせてもダメ、√3だけ掛け合わせてもダメ、√5＋√3を掛け合わせてもダメです。
そのような場合は、2つの数の間の符号を反転させたもの（プラスのときはマイナス、マイナスのときはプラス）を分母と分子に掛け合わせてください。
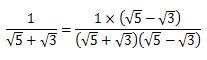
どんどん計算していきましょう。
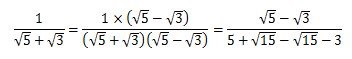
したがって、答えは
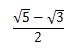
になります。
関数電卓などで計算してもらうとわかりますが、有理化する前と有理化した後の式は違ってきますが値は同じになります。
有理化した方が数が見やすくなるだけですので値の変化はありません。
なお、有理化できるものは有理化させた答えを計算ドリルやテストの答案に書かないと答えに丸がもらえないので気をつけてください。
 |
 |
 |