複素数
学習する学年:高校生
1.複素数の説明
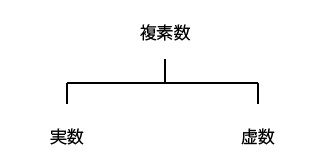
高校へ進学すると複素数という授業が始まります。
複素数とは、実数と虚数を組み合わせた数のことをいいます。
みなさんは、実数 とはどのような数のことを表すのか覚えていますか?
実数とは、整数、分数、小数をひとまとめにした数の事です。整数、分数、小数を説明しますので忘れた方は覚えてください。
- 整数とは、-2、-1、0、1、2のように私たちが日常の生活で、ものを数える時に普通に使っている数です。
- 小数とは、-7.2、0.25、9.8のように小数点を含んだ数です。
では、分数はどうかというと、小数に変換できますので小数に含まれます。
実数とはどういう数のことなのか思い出してもらったところで、次は、虚数 について説明します。
虚数という言葉は高校の数学にでてきます。中学校では勉強しませんのであまり聞きなれない言葉ですね。虚数とは、想像上の数のことをいいます。
実数とは、本当の数とか目に見える数として扱うことに対して、虚数とは、実体がないとか目に見えない数として扱います。
実数と虚数には専門用語があり、実数部(実部)をreal partといいre、虚数部(虚部)をimaginary partといいim、として表記します。
この、実数と虚数を含んだ複素数は、式で表す場合は次のようにします。
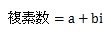
a=実部
bi=虚部
なお、aの実部は実数ですが、biの虚部のbも実数で表します。bに虚数単位のiを付け加えることで虚部として表します。
2.複素数を式で表してみましょう
それでは、複素数を実際に式で表わしてみましょう。
例えば
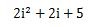
という複素数があったとします。
この複素数の式は、a+biの形にしてください。
この式は、i2が含まれていますので、虚数単位iの定義(2乗すると-1になる)である次の式
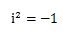
を代入すると
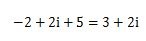
となります。
複素数を計算する時は、実部(-2+5)と虚部(+2i)に分けて計算してください。
3.複素数を複素平面(ガウス平面)に描いてみましょう
上で求めた3+2iという複素数を、複素平面(ガウス平面)に表すと下のようになります。
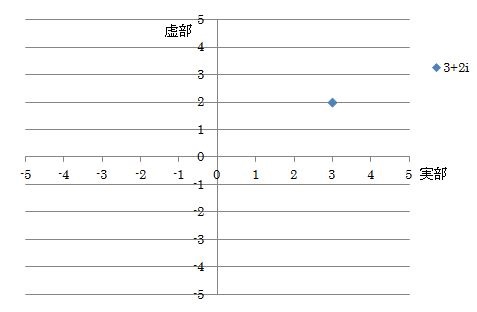
このグラフは、横軸は実部(re)、縦軸が虚部(im)となります。
このグラフが意味することは、式に虚数が含まれていると、縦軸が必要となり、数直線(横軸)だけでは数を表せられなくなるということです。
複素数は、実部と虚部を使って2次元で表すものと覚えておきましょう。
