わりざん(平方根の計算)
学習する学年:中学生
1.平方根のわりざんについて
平方根の割り算を計算する時は、平方根の掛け算を計算する時と同じように、平方根の値どうしとそれ以外の値どうしを、普通に掛けたり割ったりできます。
平方根の掛け算の計算については、こちら かけざん(平方根の計算) を見てください。
したがって、平方根の足し算や引き算の計算のようにルートの中の値を合わせなくても普通に計算ができるということです。
平方根の足し算と引き算が苦手という方は、平方根の割り算から勉強してみてください。
平方根の割り算の計算で気を付けることは、計算の最後には分数のルートの数が分母に残るので、必ず有理化をして計算結果を見やすくわかりやすくしましょう。
有理化の方法はわかりますか?
分母に平方根を含んだ分数を有理化する方法については、こちら 有理化 を見てください。
平方根の割り算は特に難しくはないと思いますので、問題を解いて計算するコツをつかんでください。
2.平方根のわりざんの計算1
上で説明した内容を頭に思い浮かべながら、次の平方根の式を計算してみましょう。
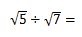
この式では、それぞれのルートの値が異なっていますが、足し算、引き算をするのではないので難しく考えないでください。
割り算を分数に変えると見た目がすっきりして計算がしやすく、わかりやすくなります。どんどん計算していきましょう。
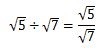
割り算を分数にしてみると、
- 分子:√5
- 分母:√7
になります。
分数にしてみると、分数の分母にルートがありますので有理化が必要になります。
有理化はわかりますか?
有理化とは、分数の分母のルートをなくす方法のことです。
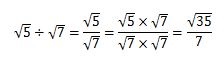
この式の場合の有理化をする方法は√7を分子と分母に掛け合わせることです。有理化してみると、√35/7になりました。
√35はこれ以上簡単にできないので、答えは、√35/7です。
平方根の割り算の計算は、平方根の足し算や引き算を計算する時のように、ルートの値を合わせなくていいので計算しやすいと思います。
3.平方根のわりざんの計算2
それでは、最後に次の平方根の式を計算してみましょう。
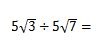
ルートの前に数字がありますが特に気にすることはありません。
割り算を分数に変えると計算しやすくなります。どんどん計算していきましょう。
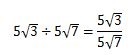
ルートの値どうし、それ以外の値どうしを分数にして普通に割ってください。
割り算を分数にしてみると、
- 分子:5√3
- 分母:5√7
となります。
なお、分数の分母にルートがありますので、最後に計算結果を有理化して答えを求めてください。
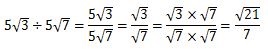
この式の場合の有理化をする方法は√7を分子と分母に掛け合わせることです。有理化してみると、√21/7になりました。
√21はこれ以上簡単にできないので、答えは、√21/7です。
有理化をすることにより分母にルートがなくなり答えが見やすくなりました。有理化できる場合は忘れずに有理化をして答えを計算しましょう。
平方根の割り算は、平方根の掛け算と同じように難しくありません。平方根の計算が難しいという方は、まずは、平方根の割り算から勉強していってください。
