倍分、変形、移項
学習する学年:中学生
1.倍分について
倍分(ばいぶん)とは、分数の場合は分母と分子に、同じ値のある数を掛け合わせることです。
ある同じ数を掛けていますので、表面上は分数の数は変化しているように見えますが、分母と分子に掛け合わせた値は同じ値ですので、分数の中身の数は掛けた前と後では同じ状態のはずです。
例えば、次の分数があるとします。
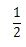
この分数の1/2の分母と分子に2をかけてみましょう。
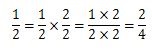
1/2の分母と分子に2を掛けて2/4になっても約分した中身は1/2ですよね。
次は、1/2の分母と分子に3を掛けてみましょう。
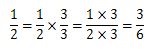
3/6となります。約分した中身は1/2ですよね。
それらの数は、
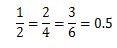
となるので、2/4でも3/6でも結局は同じ値の1/2=0.5になります。
約分は分母と分子を同じ値で割る計算方法ですが、倍分は分母と分子に同じ値を掛ける計算方法です。
ちなみに、余談ですが、ある整数を何倍かした数のことを倍数といいます。倍分と倍数は違う意味なので間違えないようにしてください。
倍分は分数の割り算の計算で分母の数を1にする時によく用いられます。約分の反対の計算方法が倍分であることを覚えておいてください。
2.分数の式を変形してみましょう
変形(へんけい)とは、未知数を含んだ式の未知数を求める時に使われる計算方法です。
未知数とは、方程式に出てくるxやyなどのことです。
それでは、未知数を含んだ分数の式を計算してみましょう。次の式をy=の形となるように変形してみましょう。
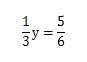
みなさんは、イコールの意味はわかりますか?
イコールの左側と右側の値は、等しい関係にあると言う意味です。
イコールの左側にある、yの前の1/3が邪魔ですね。
この1/3を消してしまいましょう。
消す方法は、1/3に3をかければ1になりますので消えます。
しかし、このままではダメです。
イコールには、イコールの左側と右側の値は等しいと言う意味がありますので右側にも3をかければ、左右のバランスがとれると思いませんか?
ですので、イコールの左側と右側にそれぞれ3をかけて計算してみます。
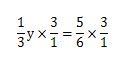
この式を計算していくとy=の答えが出てきます。
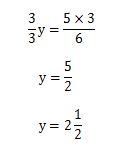
どうでしたか?計算できましたか?
いままで分数の計算がよくわからなかった方でも、なんとなく理解できたでしょうか?式を変形させて計算するコツをつかむまで何回でも練習してください。
3.移項について
移項(いこう)とは、左辺の項(イコールより左にある項)を右辺へ、右辺の項(イコールより右にある項)を左辺へ移動させることです。
この移動させる作業をすることによって、式がわかりやすくなります。
それでは、次の式を移項してみましょう。
xの項を左辺へ、それ以外は右辺へ移動してまとめてみましょう。
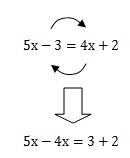
上の式をみると、移動した項の符号が変わったことに気が付きましたか?
移項にはルールがあります。移行すると、
- プラス(+)の項はマイナス(-)
- マイマス(-)の項はプラス(+)
になります。
移行をすると、符号が反転すると覚えておけば大丈夫です。
