連立1次方程式の解法2(加減法)
学習する学年:中学生
1.連立1次方程式を加減法で解く方法
連立1次方程式は、代入法か加減法を使って答えを解くことができます。
今回は、連立1次方程式の解き方の代入法ではなく、もう一つの解き方の加減法について説明します。
代入法で解く方法を勉強したい方は、こちら 連立1次方程式の解法1 をご覧ください。
加減法の説明に使う式は、連立1次方程式の解法1(代入法)の時に使った、同じ式を使って計算しますので同じ答えになります。
代入法を使うと、すんなり計算できた方もいるかと思いますが、加減法を使って解くには、少しコツが必要になります。
代入法の解き方の手順は次の通りです。
- xかyの係数を揃える
- xかyの値を計算する
加減法で解くにはどのようなことに気をつけないといけないのかと言うと、xかyの係数を同じ数にそろえなければいけないことです。
少しコツが必要ですが解き方は難しくありませんので、少し問題を解いていったら解き方が理解できると思います。
2.連立1次方程式を加減法を使って解いてみよう
それでは、次の連立1次方程式を加減法を使って解いてみましょう。
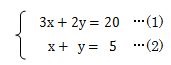
上記で説明した連立1次方程式を加減法で解く手順に従って計算してください。
まず初めは、xかyの係数を式(1)と式(2)で同じ数にそろえなければいけませんよね。
係数とは上の式の場合、3xの3、2xの2、1xの1、1yの1のことです。
xの係数を式(1)と式(2)でそろえる為に、式(2)の数を3倍してみましょう。
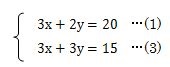
式(2)の数を3倍することによって、式(1)と式(2)のxの係数が3でそろいました。xの係数が3になった式(2)を式(3)としておきます。
この状態で、式(1)から式(3)を引くと、xの項がゼロになるのでyの値が求まると思いませんか。
計算方法は次のようになります。
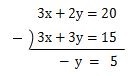
xの項の計算
- 3x-3x=0
yの項の計算
- 2y-3y=-y
定数項の計算
- 20-15=5
(xの項の計算)+(yの項の計算)=定数項の計算
- 0+(-y)=5
よって、-y=5となり、yの答えの値はy=-5になりました。
次は、yの係数を式(1)と式(2)でそろえる為に、式(2)の数を2倍してみましょう。
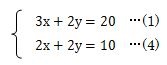
式(2)の数を2倍することによって、式(1)と式(2)のyの係数が2でそろいました。yの係数が2になった式(2)を式(4)としておきます。
この状態で、式(1)から式(4)を引くと、yの項がゼロになるのでxの値が求まると思いませんか。
計算方法は次のようになります。
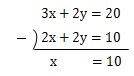
xの項の計算
- 3x-2x=x
yの項の計算
- 2y-2y=0
定数項の計算
- 20-10=10
よって、xの答えの値はx=10になりました。
xとyの値は、x=10、y=-5となり、加減法で計算しても代入法で計算しても同じ答えになりました。
ところで、加減法の計算の仕方は理解できましたか?
加減法は、xの係数かyの係数を式(1)と式(2)で同じ値にした後に引くことによりxかyを相殺しなければいけません。
係数を何倍しなければいけないのか考える必要がありますので少し面倒に思えるかもしれませんが、解き方に慣れると加減法の方が簡単に答えが導けれるようになると思います。
まずは、簡単な代入法の解き方を覚えてから加減法の解き方に慣れていってください。
