最小公倍数の求め方
学習する学年:小学生
1.最小公倍数の説明
最小公倍数とは、2つ以上の正の整数(自然数)に共通な倍数のうち最小の数のことをいいます。但しゼロは除きます。
つまり、公倍数の中で一番小さな共通する数が最小公倍数ということです。
みなさんは、倍数の意味と求め方は覚えていますか?
倍数とは、ある数を2倍、3倍、4倍、5倍などと整数倍した数のことでしたよね。
例えば、6と15の最小公倍数を求める時は、それぞれの数の倍数を求めて、6の倍数(6、12、18、24、30)と15の倍数(15、30、45、60)で共通する一番小さい数を探せば最小公倍数は求まります。
答えは30になります。
しかしながら、このように計算すると計算間違えすることもよくあり時間も掛かりますし、最小公倍数の定義だけを聞いてもどうやって解いたらいいのかさっぱりわからないという方もいますので、最小公倍数を間違いなく求めるには、機械的に次の順序にしたがって計算することをおすすめします。
- 最小公倍数を求めるそれぞれの数を素因数分解します。
- 素因数分解した数をそれぞれ重ねていきます。
- 重なっても重ならなくても数を掛け合わせます。
この順番に計算していくと簡単に最小公倍数を求めることができます。
それでは、実際に手を動かして問題を解いてみましょう。
2.最小公倍数の計算1
それでは、40と30の最小公倍数を求めてみましょう。
まず初めに行う作業は、40と30をそれぞれ素因数分解します。
素因数分解とは、ある数を素数の積で表した形のことをいいます。
素数という言葉の意味はわかりますか?
2、3、5、7、11などの約数を2つしか持っていない数のことです。
素因数分解という言葉を見ると難しそうな雰囲気がありますが、次のようにすだれ算(さかさわり算)をすれば簡単に求まります。
すだれ算とは割り算記号を逆の形にして割っていくスタイルの計算方法です。
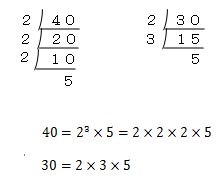
40と30を素因数分解すると、
- 40=2×2×2×5
- 30=2×3×5
となります。
次は、素因数分解した数をそれぞれ重ねていき、重なっても重なっていなくてもその数を掛け合わせます。
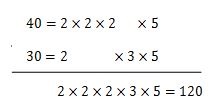
この場合は、2と2と2と3と5を掛け合わせて、2×2×2×3×5=120となります。
したがって、120が40の倍数と30の倍数で共通となる最小の数となるので、「40と30の最小公倍数は120」というのが答えです。
3.最小公倍数の計算2
最後に、8と12の最小公倍数を求めてみましょう。
この例題も上記の例題と同じ方法で計算してください。素因数分解して重なっても重ならなくても数を掛け合わせて解いていけば答えはでます。
まずは、8と12をすだれ算(さかさわり算)を使って素因数分解してください。
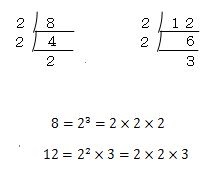
8と12を素因数分解すると、
- 8=2×2×2
- 12=2×2×3
となります。
次は、素因数分解した数をそれぞれ重ねていき、重なっても重ならなくてもその数を掛け合わせます。
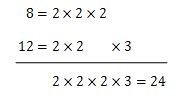
この場合は、2と2と2と3を掛け合わせて、2×2×2×3=24となります。
したがって、24が8の倍数と12の倍数で共通となる最小の数となるので、「8と12の最小公倍数は24」というのが答えです。
このように、最小公倍数を求める時は、すだれ算を使って素因数分解することがコツとなります。
素数・素因数分解がわかれば簡単に解けます。素数とは何なのかと素因数分解する方法がわからない方はしっかり覚えてください。
