数学の2次関数の式とグラフ

学習する学年：中学生

１．2次関数の式

2次関数を勉強する前に、関数とは何かわかりますか。

関数とは、未知数xの値に対するyの値の関係を表すことです。未知数xに値を代入すると答えのyの値が1つ決まることでしたよね。

今回は、関数の中の2次関数について説明します。

2次関数とは、次数が2の関数のことです。

次数とは、xという未知数が何乗になっているのかという何乗の部分の数字のことで、x²となっているものは2次といいます。

したがって、次のような関数を2次関数といいます。

• y=3x²、y=7x²、y=20x²＋8、y=-x²

2次関数の他に1次関数もあるので間違えないようにしてください

2次関数と2次方程式で意味を間違えやすいですが、2次関数とは関数で2次方程式とは方程式のことです。

2次関数はy=で表した式のこと、2次方程式はイコールが成り立つ式のことです。

2次関数は、xの値をいくつか入力するとyの値もいくつか返ってくると覚えておけばいいでしょう。

２．2次関数のグラフ

2次関数の式がわかったところで、次の2次関数の増減表とグラフを描いて、x、yの関係をみてましょう。

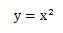
それでは、2次関数のグラフを描く為にまずは増減表を作成します。

増減表とは、式のxとyの値を求めて表にまとめたものでしたよね。y=x²のxの値を入力してyの値を求めれば増減表は作成できます。

xが－4～＋4までのxとyの値の関係について表にしてみましょう。

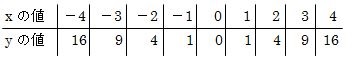
この増減表は、xが－4～＋4までの関係について計算して表にまとめました。

増減表ができたので、次はグラフを描いてみましょう。

グラフの描き方は、方眼用紙に増減表のxとyの値をプロットして、滑らかな線となるように点をどんどん結んでグラフを作っていきます。

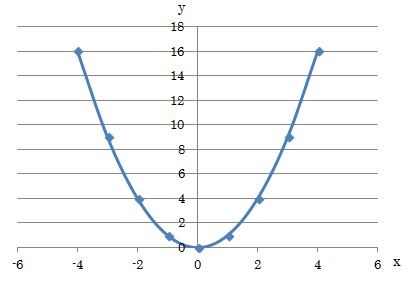
y=x²は、増減表とグラフから読み取ると、yの値はゼロを基準としてxの値が増えても減ってもyの値はどんどん大きくなっていて、そしてグラフの形は放物線になることがわかりました。

この放物線になることが、2次関数の大きな特徴になります。

このように、グラフを描く時は、増減表を作ってからグラフを描くと作業しやすいです。

これで、1次関数と2次関数の両方の式とグラフの違いが理解できたと思います。