三角比(sin, cos, tan)
学習する学年:高校生
1.sin, cos, tanって何?
高校生になると、sin(サイン)、cos(コサイン)、tan(タンジェント)の授業が始まります。
中学生までの数学の授業では、sin、cos、tanという言葉は、あまりなじみがなかったですよね。
そんな言葉なんて聞いたことがないし知らないという方もいるのではないでしょうか。
sin,cos,tanは、次のように、正弦、余弦、正接とも呼ばれています。
- sin:正弦
- cos:余弦
- tan:正接
直角三角形の3つある辺の内のそれぞれ2つの辺を使って比を表しており、三角比はsin,cos,tanを使えば定義ができます。
三角比は普段の生活では全く使う場面が見当たりませんが、高校、大学では図形の計算をする時、社会人になっても工学系の設計の仕事をする方はよく使う場面があります。
sin,cos,tanはなんだか難しそうに見えても、理屈を理解していたら難しくありません。sin,cos,tanが学校の授業に出てきてわからなかったらこの機会に意味をしっかり覚えてください。
2.sin, cos, tanを使ってみよう
それでは、下の図形の角度が30度の時の直角三角形の比をsin、cos、tanを使って表してみましょう。
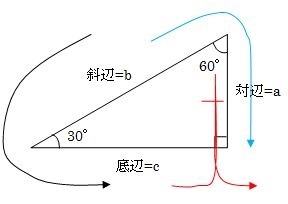
sin何度, cos何度, tan何度という角度は、左端の角度を基準とします。
また、sin、cos、tanを求める時は、三角形の比を使います。
直角三角形の左端の角度が30度の時のそれぞれの辺の長さの比を覚えていますか?
三角形の比についてよくわからない方は、三角比(30°,45°,60°) をみてください。
それでは、sin30°(サイン30度)、cos30°(コサイン30度)、tan30°(タンジェント30度)の求め方を説明していきます。
- sin30°の求め方
上の直角三角形に描いてある水色の線を見てください。
sinのsを筆記体で描くイメージで、描き始めの辺(斜辺)を分母、描き終わりの辺(対辺)を母子に置きます。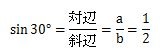
したがって、sin30°=1/2です。
では、sinθは何を求めているのかというと高さ(対辺の長さ)です。
- cos30°の求め方
上の直角三角形に描いてある黒色の線を見てください。
cosのcを描くイメージで、描き始めの辺(斜辺)を分母、描き終わりの辺(底辺)を母子に置きます。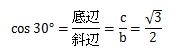
したがって、cos30°=√3/2です。
では、cosθは何を求めているのかというと横の長さ(底辺の長さ)です。
- tan30°の求め方
上の直角三角形に描いてある赤色の線を見てください。
tanのtを筆記体で描くイメージで、描き始めの辺(底辺)を分母、描き終わりの辺(対辺)を母子に置きます。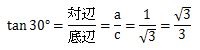
答えは有理化してください。
したがって、tan30°=√3/3です。
では、tanθは何を求めているのかというと直線の傾き(斜辺の傾き)です。
ここで説明した角度が30度の時の他に、45度、60度もよく出てきます。
直角三角形の左端の角度が45度(sin45°、cos45°、tan45°)と60度(sin60°、cos60°、tan60°)の時も同じ要領で各人で三角比を一回求めてくだい。
下に角度ごとにまとめたsin、cos、tanをまとめました。勉強の参考にしてください。
| 三角比 | 角度 | ||||
|---|---|---|---|---|---|
| 0° | 30° | 45° | 60° | 90° | |
| sin | 0 | 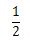 | 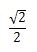 | 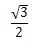 | 1 |
| cos | 1 | 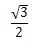 | 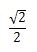 | 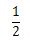 | 0 |
| tan | 0 | 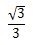 | 1 | 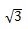 | なし |
注意することは、sin0°=0、cos90°=0、tan0°=0、tan90°=なし、ですので間違えないようにしてください。
