分数と小数の構造・種類
学習する学年:小学生
1.分数の構造
分数とは、分母と分子という数を使って表されている数のことです。
ところで、分母と分子は何の数のことかわかりますか?
分数の構造は次のようになっていますのでしっかり覚えてください。

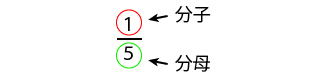
分数の下の数は分母、上の数は分子といわれていて、この分母と分子で表現されている数が分数となります。
例えば、次の分数を見ていきましょう。
5分の1は分数でしょうか?
分数の考え方は、5分の1という数は、5という数は分母、1という数は分子です。
分数の構造を作らないといけないので、5を分母、1を分子の位置に当てはめてください。
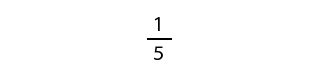
5分の1は、分母と分子がありますので分数です。
マイナス2分の1は分数でしょうか?
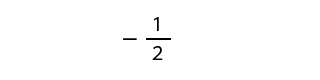
マイナス2分の1も分母と分子がありますので分数です。
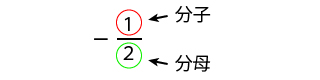
このように、マイナスの符号があってもなくても分数には関係ありません。数が分母と分子の構造になっていれば分数です。
2.分数の種類
分数には、真分数、仮分数、帯分数の3種類があります。

- 真分数(しんぶんすう):分子よりも分母の数の方が大きい分数のことです。
- 仮分数(かりぶんすう):分子よりも分母の数の方が小さい分数のことです。
- 帯分数(たいぶんすう):分数の前に数が書いてある分数のことです。
なお、5/5のように分子と分母の数が同じ時は仮分数に分類されます。
また、分数は全体の量に対する部分的な量を表しているので、その数の量を感覚的に理解することを容易にするために使われます。
例えば、次の分数と小数の数を見てみましょう。
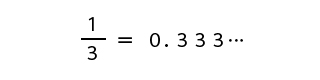
この分数は、3分の1(全体が3という中の1つという意味)ですが、小数で表すと1÷3=0.333…になります。
※分数は小数に置き換えることができます。
どちらの数の方が、ぱっと見て感覚的にわかりやすいでしょうか?
分数で表した方がわかりやすいと思いませんか。
このように、わかりやすさも意識して分数は使われています。
3.小数の構造
小数とは、次のように小数点を使って表された数のことです。
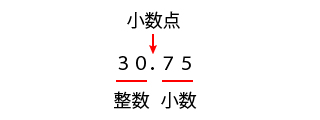
小数は整数の部分と小数の部分を小数点で区切って表されているので、整数、小数点、小数の3つの部分を持つ構造をしています。
小数のそれぞれの桁の読み方は、小数点を基準にしてそれよりも前は整数の位、後は小数の位として読みます。
例えば、30.75の数のそれぞれの桁の読み方は、
- 3:十の位
- 0:一の位
- 7:小数第一位(1/10の位)
- 5:小数第二位(1/100の位)
となります。
算数の勉強を始めた時に学んだ整数という数は、
- -3、-2、-1、0、1、2、3
のように、数と数の間が1ずつ開いていましたよね。
しかし、小数の場合はどうでしょうか。
小数は、
- -1.5、0.2、7.8
のように、整数よりも数と数との間隔をさらに細かく表現できます。
小数がよくわからないという方は整数と小数の構造の違いを理解してください。
4.小数の種類
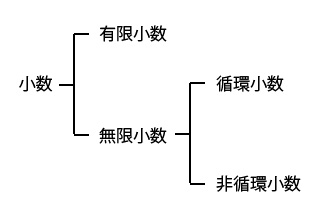
小数には、次の有限小数と無限小数の2種類があり、無限小数はさらに循環小数と非循環小数の2種類に分けることができます。
- 有限小数
- 小数点以下の数が有限な数。要するに、小数点以下の数は終わりがある数のことです。
例:3.2、0.5、0.25 - 無限小数
- 小数点以下の数が無限に続く数。要するに、小数点以下の数は終わりがなくずっと続く数のことです。なお、無限小数は、循環小数と非循環小数に分けられます。
例:0.33333…、0.090909…、1.4142135…、3.141592… - 循環小数
- 小数点以下の数が規則に従って繰り返し現れる数。
例:0.33333…、0.090909… - 非循環小数
- 小数点以下の数が規則に従って繰り返されなくて現れる数。
例:1.4142135…、3.141592…
有限小数、無限小数、循環小数についての詳しい説明は、有理数、無理数 の項を見てください。
また、上記の分数の説明のように分数は小数に置き換えることができますよね。
では、小数から分数に置き換えることは可能だと思いますか?
実は、小数から分数に置き換えることができるものもあれば、小数から分数に置き換えることができないものもあります。
例えば、
- 0.1=1/10
- 0.2=1/5
- 0.3=3/10
のような有理数は小数から分数に置き換えることができます。
しかしながら、√(ルート)やπ(パイ) などのような無理数は分数に置き換えることはできないので気を付けてください。
