有理数
学習する学年:中学生
1.有理数の説明
有理数(ゆうりすう)とは、整数÷整数(整数分の整数)のような次の形で表される数のことをいいます。

但し、1/0、2/0のような分母が0の時は分数で表すことができませんので、分母が0ではない整数(1、2、3、4、5・・・)に限ります。
例えば、
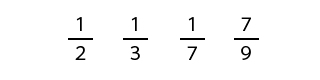
のように表されるこれらの数はすべて有理数といいます。
また、-1/2、-1/3、2/2=1、3/3=1などの数も有理数です。
自然数や整数の範囲では一部の割り算ができませんでしたが、有理数の範囲では割り算ができるようになりました。
整数がわからない方は、有理数を勉強する前に整数を勉強してください。
有理数のことをまとめますと、整数(負の整数、ゼロ、正の整数)、整数ではない有理数(分数)のことを言います。
なお、整数ではない有理数(整数分の整数)を小数に置き換えると、有限小数、無限小数、循環小数になります。
2.有限小数の説明
有限小数とは、小数点以下の数字が有限となっている小数のことです。
例えば、次の分数を小数にした数を見てください。
この小数は、小数点以下の数字は5で終わっています。
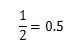
このように、数が有限の場合は有限小数といいます。
3.無限小数の説明
無限小数とは、小数点以下の数字が同じ数字で永遠に続いている小数のことです。
例えば、次の分数を小数にした数を見てください。
この小数は、小数点以下の数字は3が永遠に続きます。
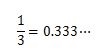
このように、数が無限に続く場合は無限小数といいます。
4.循環小数の説明
循環小数とは、小数点以下の数字が規則性を持って永遠に続いている小数のことです。
例えば、次の分数を小数にした数を見てください。
この小数は、小数点以下の数字は142857が繰り返し現れて永遠に続きます。
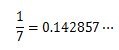
このように、規則性がある数が続く場合は循環小数といいます。
ここまで説明してきましたように、有限小数でも、無限小数でも、循環小数でも分数で表せられる数を有理数といいます。
