小数を分数に変換する方法
学習する学年:小学生
1.小数を分数に変換した方が計算が簡単
小学生の高学年になると分数どうしの計算と小数どうしの計算が始まります。
分数どうしの計算でも小数どうしの計算でもどちらでも慣れないと大変です。さらに、分数と小数が混ざり合った計算も出てくるようになりさらに計算が大変になります。
分数と小数が混ざり合った計算方法は、小数を分数に変換して分数どうしにする、又は分数を小数に変換して小数どうしにしなければ解くことができません。
どちらの方法を使っても大丈夫ですが、分数を少数に変換して解くと無限小数(1/3=0.3333…など)になってしまって計算ができなくなる恐れがあるので、小数を分数に変換して解いた方が簡単だと思います。
つまり、特別な数を除いてはどのような小数でも分数に変換できるので分数にしてから計算することをおすすめします。
2.小数を分数にする方法
小数を分数に変換する方法を見ていきましょう。
小数を分数に変換する時は、次のようなルールがあるので覚えてください。
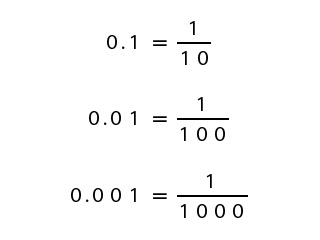
0.1は小数点以下の桁数が1桁なので、分母は0を1つつけて1/10となります。
0.01は小数点以下の桁数が2桁なので、分母は0を2つつけて1/100となります。
0.001は小数点以下の桁数が3桁なので、分母は0を3つつけて1/1000となります。
小数点以下の桁が何桁なのか数えてから分母に10や100や1000を配置すると小数を分数に置き換えることができます。
このように、小数から分数に変換する時は、上記のルールを使って計算するのがコツです。計算をスムーズに行う為に覚えておいてください。
3.小数を分数にする練習問題1
小数を分数に変換する方法がわかったところで練習問題を解いてみましょう。
次の小数を分数に変換するといくつになりますか。

0.5は小数点以下の桁が1桁なので、分母は0を1つつけて1/10となります。
しかしながら、0.5の5の数がまだ使っていませんよね。小数点以下の数は分子に配置するものなので次のように5を分子に載せてください。
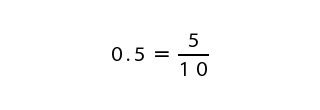
分子は5、分母は10なので、0.5=5/10となりましたが、5で約分できそうなので約分します。
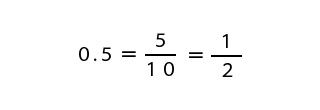
したがって、0.5=1/2となりました。約分できるものは約分して答えを出してください。
4.小数を分数にする練習問題2
次の小数を分数に変換する練習問題を解いてみましょう。

0.12は小数点以下の桁は2桁なので、分母は0を2つつけて1/100となります。
しかしながら、0.12の12の数がまだ使っていませんよね。小数点以下の数は分子に配置するものなので次のように12を分子に載せてください。
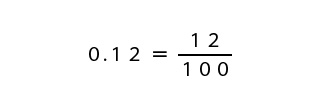
0.12=12/100となりましたが、4で約分できそうなので約分します。
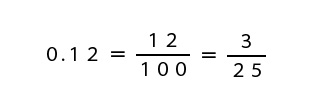
したがって、0.12=3/25となりました。約分できるものは約分して答えを出してください。
5.小数を分数にする練習問題3
次の小数を分数に変換する練習問題を解いてみましょう。

3.6は小数点以下の桁は1桁なので、分母は0を1つつけて1/10となります。
しかしながら、3.6の整数部分の3と小数部分の6の数がまだ使っていませんよね。小数点以下の数はいままで通り分子に配置するものなので6を分子に載せてください。
では、整数部分はどうするのかというと帯分数となりますので3は分数の前に配置してください。
3.6を分数にすると次のようになります。
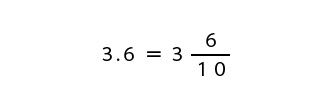
3.6=3と6/10となりましたが、2で約分できそうなので約分します。
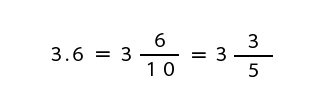
したがって、3.6=3と3/5となりました。約分できるものは約分して答えを出してください。
なお、今までの方法と少し違うやり方でも小数を分数にすることができます。
3.6の小数点以下の桁数は分母の0の数、3.6の数は小数点を取り除いて分子の数にしても計算できます。
分母の0の数は1つ、分子は36を使います。
計算すると次のようになりました。
- 36/10=18/5=3と3/5
同じ数になりました。どちらの方法でもいいのでやりやすい方で計算してください。
小数を分数に変換する方法を覚えて分数の計算を得意になってください。
